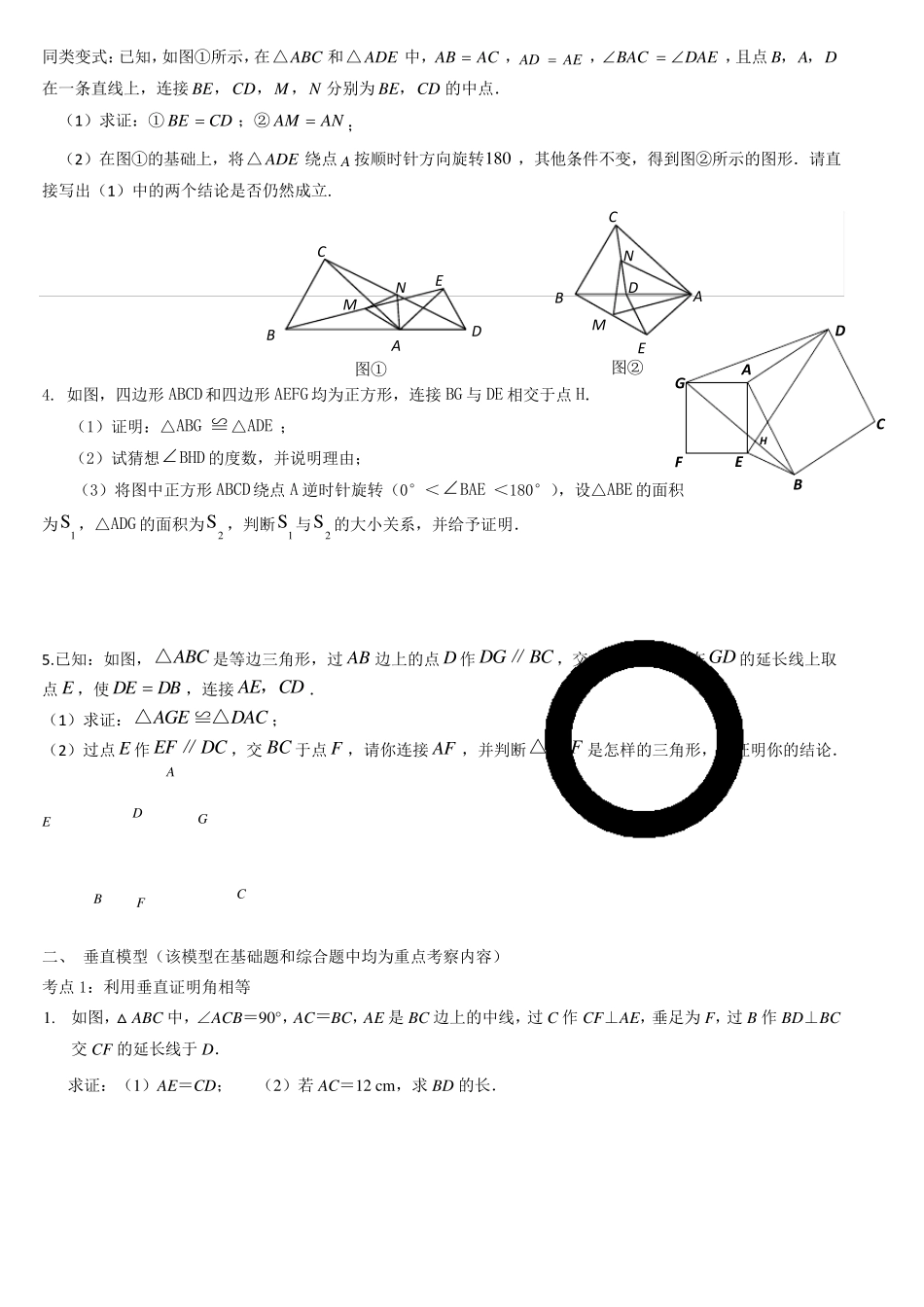
B A O D C E 图8 济南初中数学压轴 --------姜姜老师 北师大版七年级下三角形综合题归类 一、 双等边三角形模型 1. (1)如图7,点O 是线段AD 的中点,分别以AO 和DO 为边在线段AD 的同侧作等边三角形O AB 和等边三角形O CD,连结AC 和BD,相交于点E,连结BC.求∠AEB 的大小; (2)如图8,ΔO AB 固定不动,保持ΔO CD 的形状和大小不变,将ΔO CD 绕着点O 旋转(ΔO AB 和ΔO CD 不能重叠),求∠AEB 的大小. 同类变式: 如图a,△ABC 和△CEF 是两个大小不等的等边三角形,且有一个公共顶点C,连接 AF 和BE. (1)线段AF 和BE 有怎样的大小关系?请证明你的结论; (2)将图a 中的△CEF 绕点C 旋转一定的角度,得到图b,(1)中的结论还成立吗?作出判断并说明理由; (3)若将图a 中的△ABC 绕点C 旋转一定的角度,请你画出一个变换后的图形c(草图即可),(1)中的结论还成立吗?作出判断不必说明理由. 图c 3. 如图9,若△ABC 和△ ADE 为等边三角形,,M N分别为,EB CD 的中点,易证: CDBE,△ AMN是等边三角形. (1)当把△ADE 绕 A 点旋转到图10 的位置时,CDBE是否仍然成立?若成立,请证明;若不成立,请说明理由; (2)当△ADE 绕 A 点旋转到图11 的位置时,△AMN是否还是等边三角形?若是,请给出证明,若不是,请 说 明 理由. 图9 图10 图11 C B O D 图7 A E 同类变式:已知,如图①所示,在ABC△和ADE△中,ABAC,ADAE,BACDAE ,且点BAD,,在一条直线上,连接BECDMN,,,分别为BECD,的中点. (1)求证:①BECD;② ANAM ; (2)在图①的基础上,将ADE△绕点A 按顺时针方向旋转180 ,其他条件不变,得到图②所示的图形.请直接写出(1)中的两个结论是否仍然成立. 4. 如图,四边形ABCD和四边形AEFG均为正方形,连接BG 与DE 相交于点H. (1)证明:△ABG ≌△ADE ; (2)试猜想 BHD 的度数,并说明理由; (3)将图中正方形ABCD绕点A 逆时针旋转(0°< BAE <180°),设△ABE 的面积 为1S ,△ADG 的面积为2S ,判断1S 与2S 的大小关系,并给予证明. 5.已知:如图,ABC△是等边三角形,过 AB 边上的点D 作 DGBC∥,交AC 于点G ,在GD 的延长线上取点E ,使 DEDB,连接AECD,. (1)求证:AGEDAC△≌△; (2)过点E 作 EFDC∥,交BC 于点F ,请你连接AF ,并判断AEF...