时间序列模型VIP免费

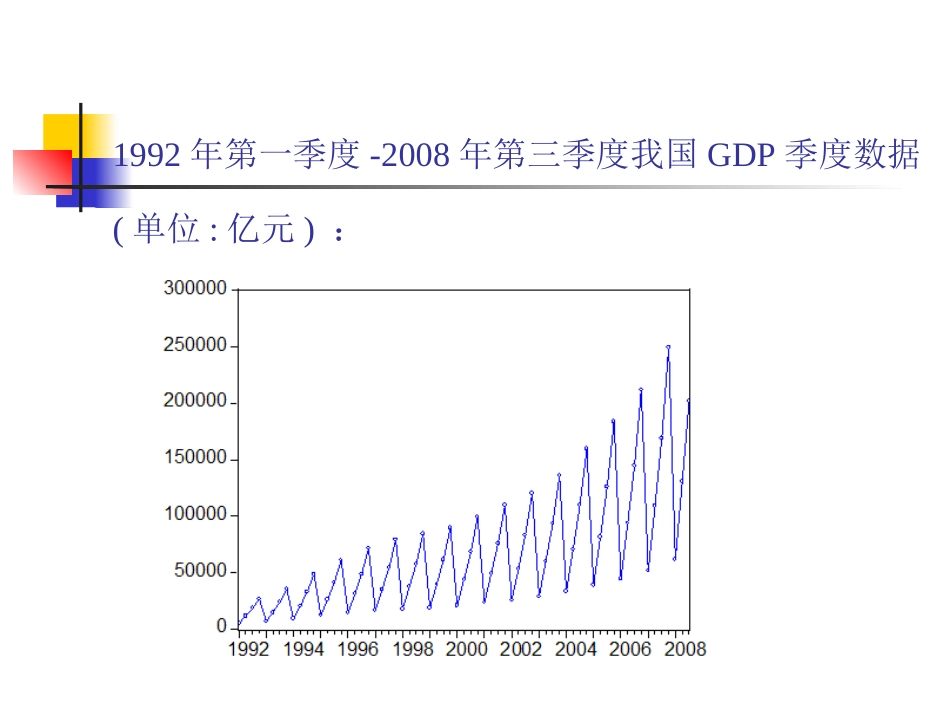
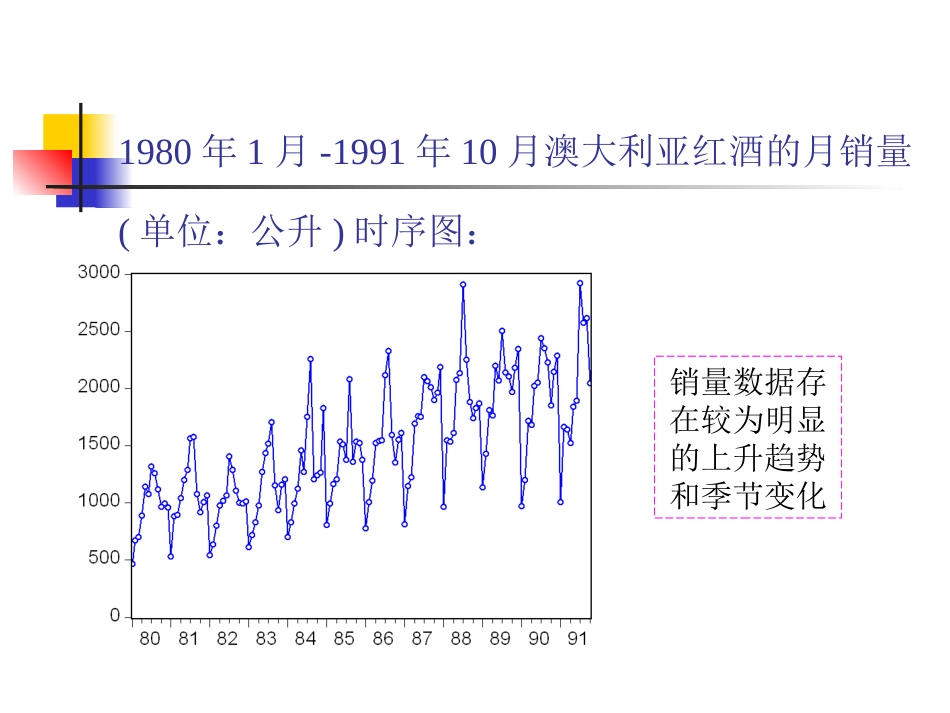
季节时间序列模型SARIMA模型1992年第一季度-2008年第三季度我国GDP季度数据(单位:亿元)：1980年1月-1991年10月澳大利亚红酒的月销量(单位：公升)时序图：销量数据存在较为明显的上升趋势和季节变化季节时间序列(SARIMA)模型在某些时间序列中，由于季节性变化(包括季度、月度、周度等变化)或其他一些固有因素的变化，会存在一些明显的周期性，这类序列称为季节性序列。在经济领域中，季节性序列更是随处可见。如季度时间序列、月度时间序列、周度时间序列等。描述这类序列的模型之一是季节时间序列模型(seasonalARIMAmodel)，用SARIMA表示。较早文献也称其为乘积季节模型(multiplicativeseasonalmodel)。季节时间序列的重要特征表现为周期性。在一个序列中，如果经过S个时间间隔后观测点呈现出相似性，比如同处于波峰或波谷，我们就说该序列具有以S为周期的周期特性。一般，季度资料的一个周期表现为一年的四个季度，月度资料的周期表现为一年的12各月，周资料表现为一周的7天或5天。处理季节性时间序列的一个重要工具：季节差分：可消除周期性变化对于非平稳季节性时间序列，有时需要进行D次季节差分之后才能转换为平稳的序列。季节时间序列的重要特征11ssssttttsSBXBXXX步差分1DDsSttXBX随机季节模型乘积季节模型季节时间序列模型季节性SARIMA(P,D,Q)模型：D为季节差分阶数，P为季节自回归的阶数，Q为季节移动平均的阶数U(BS)为季节自回归多项式，V(BS)为季节移动平均多项式EVIEWS上的实现：随机季节模型212212111DSSSttSSSPSPSSSQSQUBBXVBUBBBBVBBBB,ijSARiSSMAjS消除了序列在不同周期相同周期点上的季节相关成分乘积季节模型使用场合：季节序列既有季节效应又有长期趋势效应模型结构：ARIMA(p,d,q)×(P,D,Q)2122122122121111()1()1SdDSSttDddDSSSSSPSPSSSQSQppqqBUBXBVBBBUBBBBVBBBBBBBBBBBB，其中iiiiEVIEWSSARiSSMAiSARiMAi实现：乘积季节模型ARIMA(p,d,q)×(P,D,Q)说明：Φ(B)和Θ(B)用来消除同一周期的不同周期点之间的相关性；U(BS)和V(BS)用来消除不同周期的同一周期点之间的相关性；一般：d≤2，D≤1P,Q≤1一般作一次季节差分后，(偏)自相关系数在kS处还存在较强的相关性时，用乘积季节模型。SdDSSttBUBXBVB拟合1948—1981年美国女性月度失业率序列差分平稳一阶、12步差分一阶12步差分后序列自相关图一般作一次季节差分后，(偏)自相关系数在kS处还存在较强的相关性时，用乘积季节模型模型定阶ARIMA(1,1,1)×(0,1,1)12模型定阶是多次尝试的结果乘积季节模型拟合模型定阶ARIMA(1,1,1)×(0,1,1)12参数估计121210.4591110.82410.586ttBBBXBBSdDSSttBUBXBVB模型检验：参数显著残差为白噪声序列模型方程：乘积季节模型拟合效果图黑点为序列观察值，红线为模型拟合值