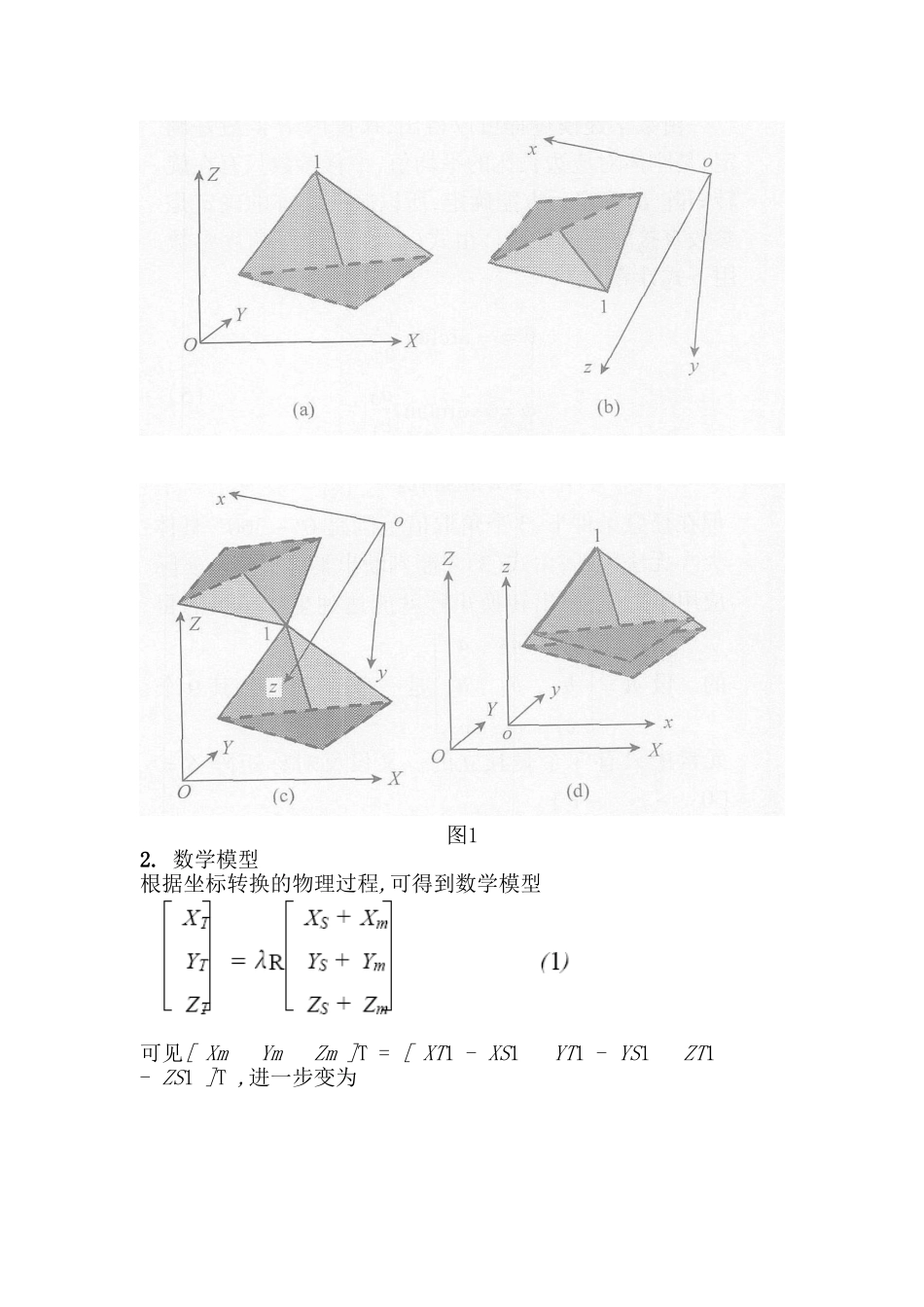
关于三维坐标转换参数的讨论摘要:首先对坐标转换的物理意义进行解释,又把传统3个旋转角参数用反对称矩阵的3个元素代替,推出用3个和4个公共点直接计算转换参数的严密公式,在此基础上推导出严密的线性化公式。由于不用进行三角函数计算,只用简单加减乘除,也不用迭代计算,所以该模型计算速度快。关键词:三维坐标转换;转换参数;转换矩阵;反对称矩阵;罗德里格矩阵一、引言三维直角坐标转换中,采用7参数Bursa2Wolf模型、Molodensky模型和武测模型[1],当在两坐标系统下有3个公共点,就可惟一解算出7个转换参数;多余3个公共点时,就要进行平差计算,转换参数的初值(特别是旋转角)的大小,直接影响平差系统稳定性和计算速度,有时使得解算的参数均严重偏离其值[2]。随着移动测图系统(MobileMappingSystem,简称MMS)技术的成熟和应用,对运动载体(飞机、轮船、汽车等)姿态的测量(GPS+INS)也越来越多[3~5],任意角度的3维坐标转换计算也越来越多。在平台上安装3台或4台GPS接收机,来确定运动载体的位置和空间姿态,这时的旋转角可以说是任意的,取值范围是-180°至180°,就需要准确计算转换参数模型,适应于任意旋转角的坐标转换。本文在解释坐标转换的物理意义的基础上,导出3维坐标转换7参数直接计算的模型,以旋转矩阵的确定为核心,导出了3点法和4点法(两坐标系统下公共点数),用反对称矩阵和罗德里格矩阵性质推出的公式严密,该模型计算速度快。二、三维坐标转换的物理意义和数学模型1.物理意义如图1所示,在两坐标系统下有4个公共点,在不同坐标系统内,看成四面的刚体,如图1(a),(b)坐标转换的物理意义就是通过平移、旋转和缩放,使两个刚体大小和形状完全相同。具体过程是,设公共点1为参考点,将图1(b)坐标轴和刚体平移,与对应的图1(a)刚体的点1重合,如图1(c),平移量为[uvw]T;然后以点1为顶点,绕3轴旋转,使两坐标系统的坐标轴平行,以参考点为顶点的边重合,其他各边平行,两刚体是相似体,只是大小不同,如图1(d);最后进行缩放,使两刚体大小也相同。这样两坐标系统和3个轴重合,原点统一,从而形成坐标系统转换。图12.数学模型根据坐标转换的物理过程,可得到数学模型可见[XmYmZm]T=[XT1-XS1YT1-YS1ZT1-ZS1]T,进一步变为式(2)左边是目标坐标系统下的坐标,右边(下标为S)表示原坐标系统下坐标;[ΔXΔYΔZ]T=R[XmYmZm]T为平移因子,其意义是参考点旋转后的坐标;λ为尺度因子;R为坐标转换旋转矩阵,或转换矩阵,R=R3R2R1,R1是把原坐标绕Z轴旋转θ角得到的旋转矩阵,R2是绕新的X轴旋转<得到的旋转矩阵,R3是绕新Y轴旋转ψ得到的旋转矩阵。(3)所以(4)习惯上称ΔX,ΔY,ΔZ,λ,θ,<,ψ为7参数,后3个称为旋转参数或角度参数。3.模型参数确定的分析由数学建模过程可以得出,尺度因子λ最好确定,是刚体对应边长比的平均值,平移参数只有在旋转矩阵R确定后方能确定,所以旋转矩阵的确定是参数直接解算的核心。由式(4)可知,3个角度参数用下式计算(5)但在任意条件下,3个角取值范围是0°~360°,具体大小无法判断,由式(3)才能判断出具体大小。实际应用中,只要解出转换矩阵就能达到坐标转换的目的。设是一个正交矩阵,其9个元素中只有3个是独立的。又设反对称矩阵,其元素是独立的。R由S构成罗德里格矩阵[6](6)其中Δ=1+a2+b2+c2。本文就是以反对称矩阵和罗德里格矩阵性质建立直接计算的公式。三、3点法计算转换参数公式在已知两坐标系统下3个公共点计算7个参数的方法称为3点法,其计算过程如下。1.反对称矩阵和罗德里格矩阵性质其中,I是3阶单位阵。2.转换参数直接解算通过上述可知,转换参数的确定关键是旋转矩阵的确定,以下是根据反对称矩阵和罗德里格的性质,由3个点计算转换参数的公式推导。由式(2),由公共点1,2可列两组6个方程,用点2方程减去点1方程,消去平移参数,并把式(7c)代入或(8)展开整理后得(9)上式只有两个独立方程,不能解出3个未知数,用点1,3可得一组方程,和式(9)联合,取3个(10)式中,u2=λXS21+XT21,v2=λYS21+YT21,w2=λZS21+ZT21,u3=λXS31+XT31,v3=λYS31+YT31(11)式中,ΔH=u3v2w2-u2v3w2,由式(7a)就可计算出转换矩阵,由式(2)可得到平移参数(12)四、算例以3点计算为例,表1列出原坐标系统和目标系统下3个公共...