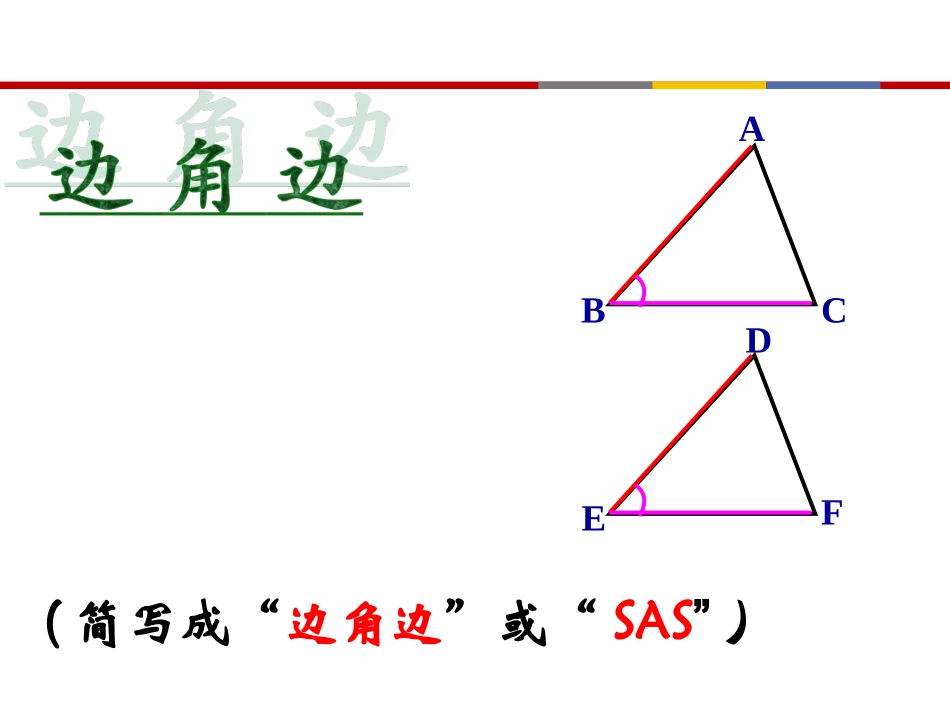
主讲老师——邓颖全等三角形关于“手拉手模型”的那点事(简写成“边边边”或“SSS”)DEFABC全等判定的复习(简写成“边角边”或“SAS”)DEFABC(简写成“角边角”或“ASA”)DEFABCDEFABC(简写成“角角边”或“AAS”)(简写成“HL”)直角三角形中:直角三角形中:HLHL例1.如图,已知△ABC与△ADE中,AB=AC,AD=AE.且∠BAC=∠DAE,求证:△ABD≌△ACE合作探究1:复杂图形中找全等三角形合作探究2:动态模型中找全等三角形,见“几何画板”归纳总结:手拉手模型——两个等腰三角形共顶点的模型条件:在△ABC与△ADE中,AB=AC,AD=AE,且∠BAC=∠DAE,结论:△ABD≌△ACE形象记忆:左手拉左手,右手拉右手例2.已知△ABC与△AEF中,AB=AC,AE=AF.且∠BAC=∠EAF,求证:(1)△ABE≌△ACF(2)∠BAC=∠BDC例题演练,精当点评练习1:△ABC与△AED均为等边三角形,点D在线段BC上,过点E作EF∥BC交AB于点F,连接BE.求证:△BEF为等边三角形师生互动,尝试练习练习.已知△ABC与△AEF中,AB=AC,AE=AF.且∠BAC=∠EAF=90°,求证:∠BDC=90°当堂检测,及时反馈课堂小结这节课你收获了什么?