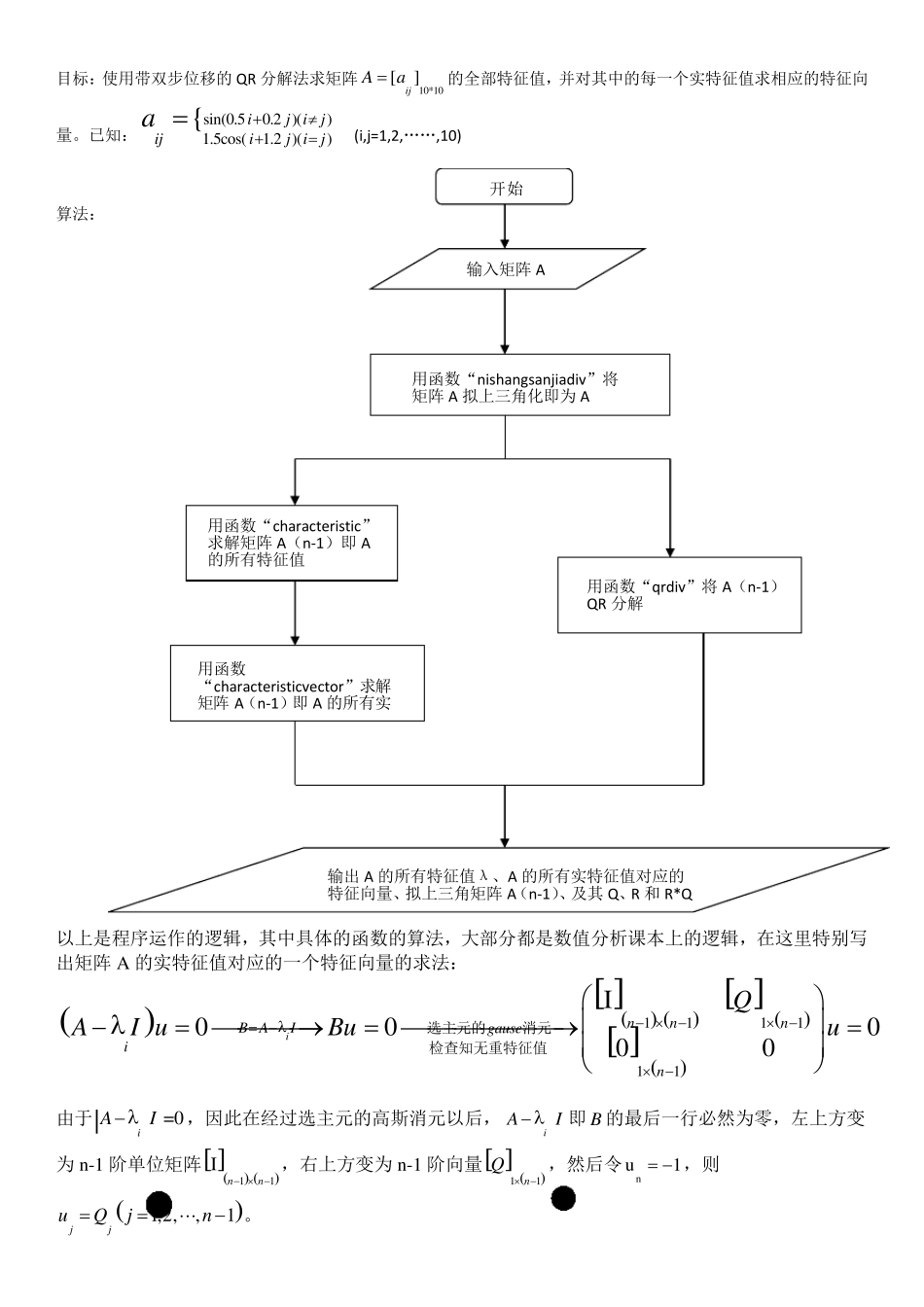
目标:使用带双步位移的QR 分解法求矩阵10*10[]ijAa的全部特征值,并对其中的每一个实特征值求相应的特征向量。已知:sin(0.50.2 )()1.5cos(1.2 )(){ij ijijij ija (i,j=1,2,……,10) 算法: 以上是程序运作的逻辑,其中具体的函数的算法,大部分都是数值分析课本上的逻辑,在这里特别写出矩阵A 的实特征值对应的一个特征向量的求法: 111111I00000innnB AIgauseinQAI uBuu 选主元的消元检查知无重特征值由于=0iAI,因此在经过选主元的高斯消元以后,iAI即B 的最后一行必然为零,左上方变为n-1 阶单位矩阵 11Inn ,右上方变为n-1 阶向量 11nQ ,然后令nu1 ,则1,2,,1jjuQjn。 开始 输入矩阵A 用函数“nishangsanjiadiv”将矩阵A 拟上三角化即为A用函数“characteristic”求解矩阵A(n-1)即A的所有特征值 用函数“qrdiv”将A(n-1)QR 分解 用函数“characteristicvector”求解矩阵A(n-1)即A 的所有实输出A 的所有特征值λ、A 的所有实特征值对应的特征向量、拟上三角矩阵A(n-1)、及其Q、R 和 R*Q 这样即求出所有A 所有实特征值对应的一个特征向量。 #include #include #include #define N 10 #define E 1.0e-12 #define MAX 10000 //以下是符号函数 double sgn(double a) { double z; if(a>E) z=1; else z=-1; return z; } //以下是矩阵的拟三角分解 void nishangsanjiaodiv(double A[N][N]) { int i,j,k; int m=0; double d,c,h,t; double u[N],p[N],q[N],w[N]; for(i=0;i