函数、极限、连续重要概念公式定理VIP免费

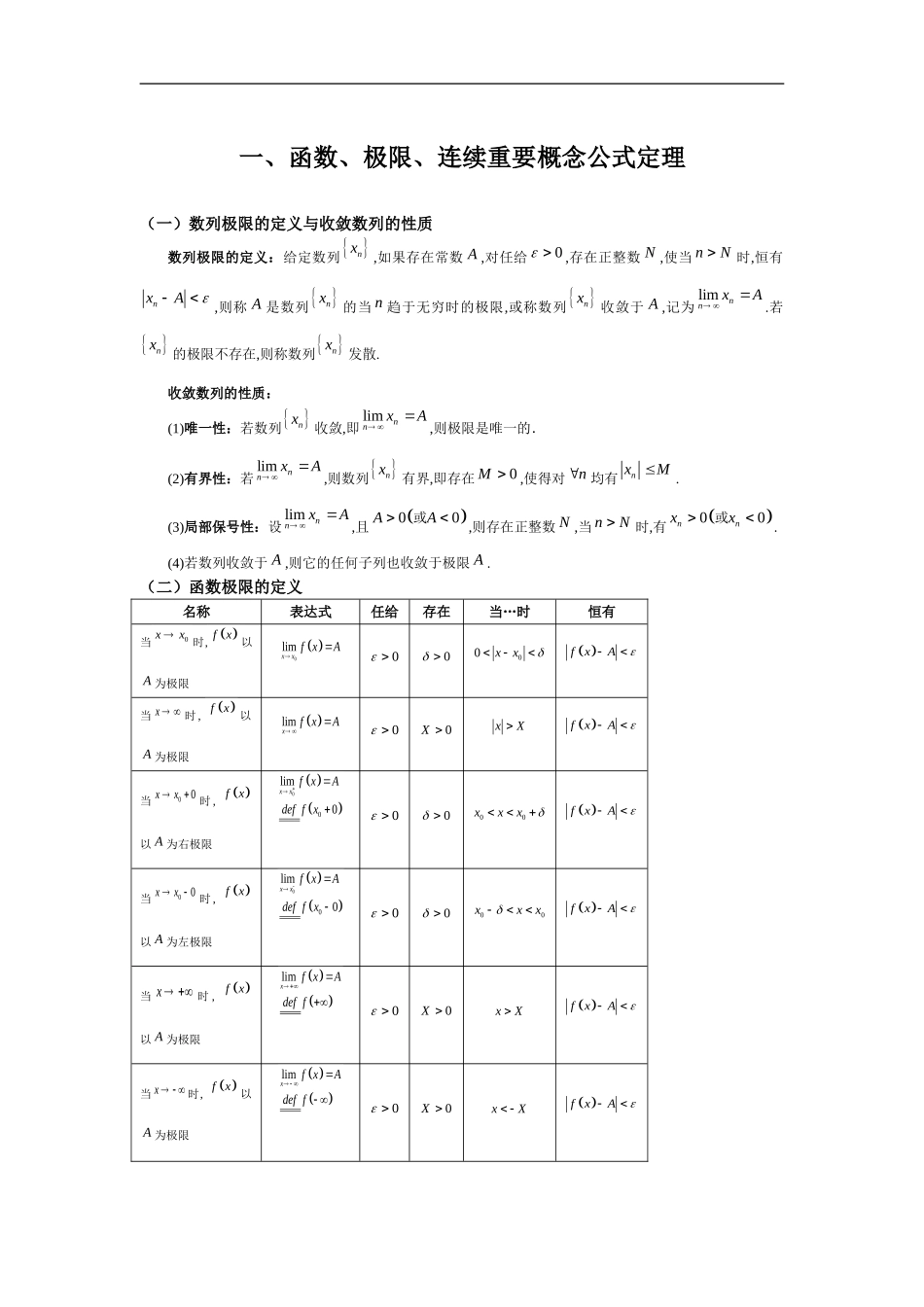
一、函数、极限、连续重要概念公式定理（一）数列极限的定义与收敛数列的性质数列极限的定义：给定数列nx,如果存在常数A,对任给0,存在正整数N,使当nN时,恒有nxA,则称A是数列nx的当n趋于无穷时的极限,或称数列nx收敛于A,记为limnnxA.若nx的极限不存在,则称数列nx发散.收敛数列的性质：(1)唯一性：若数列nx收敛,即limnnxA,则极限是唯一的．(2)有界性：若limnnxA,则数列nx有界,即存在0M,使得对n均有nxM.(3)局部保号性：设limnnxA,且00AA或,则存在正整数N,当nN时,有00nnxx或.(4)若数列收敛于A,则它的任何子列也收敛于极限A.（二）函数极限的定义名称表达式任给存在当…时恒有当0xx时,fx以A为极限0limxxfxA0000xxfxA当x时,fx以A为极限limxfxA00XxXfxA当00xx时,fx以A为右极限00lim0xxfxAdeffx0000xxxfxA当00xx时,fx以A为左极限00lim0xxfxAdeffx0000xxxfxA当x时,fx以A为极限limxfxAdeff00XxXfxA当x时,fx以A为极限limxfxAdeff00XxXfxA（三）函数极限存在判别法(了解记忆)1．海涅定理：0limxxfxA对任意一串0nxx0,1,2,nxxn,都有limnnfxA．2.充要条件：(1)000lim()limlimxxxxxxfxAfxfxA;(2)lim()lim()lim()xxxfxAfxfxA.3.柯西准则：0limxxfxA对任意给定的0,存在0,当100xx,200xx时,有12fxfx.4.夹逼准则：若存在0,当00xx时,有)()()xfxx（,且00lim()lim(),xxxxxxA则0lim()xxfxA.5.单调有界准则：若对于任意两个充分大的1212,,xxxx,有12fxfx(或12fxfx),且存在常数M,使fxM(或fxM),则limxfx存在.（四）无穷小量的比较(重点记忆)1.无穷小量阶的定义,设lim()0,lim()0xx.(1)若()lim0()xx,则称()x是比)x（高阶的无穷小量.(2)()lim,())()xxxx若则是比（低阶的无穷小量.(3)()lim(0),())()xccxxx若则称与（是同阶无穷小量.(4)()lim1,())()xxxx若则称与（是等价的无穷小量,记为()()xx.(5)()lim(0),0,())()kxcckxxkx若则称是（的阶无穷小量2.常用的等价无穷小量(命题重点,历年必考)当0x时,sinarcsintan~,arctanln(1)e1xxxxxxx211cos~2(1)1~xxxx是实常数（五）重要定理(必记内容,理解掌握)定理1000lim()()()xxfxAfxfxA.定理200lim()()(),lim()0xxxxfxAfxAaxax其中.定理3(保号定理)：0lim(),0(0),0xxfxAAA设又或则一个,当000(,),()0(()0)xxxxxfxfx且时，或.定理4单调有界准则：单调增加有上界数列必有极限;单调减少有下界数列必有极限.定理5(夹逼定理)：设在0x的领域内,恒有)()()xfxx（,且00lim()lim(),xxxxxxA则0lim()xxfxA．定理6无穷小量的性质：(1)有限个无穷小量的代数和为无穷小量;(2)有限个无穷小量的乘积为无穷小量;(3)无穷小量乘以有界变量为无穷小量．定理7在同一变化趋势下,无穷大量的倒数为无穷小量;非零的无穷小量的倒数为无穷大量．定理8极限的运算法则：设lim,limfxAgxB,则(1)lim(()())fxgxAB(2)lim()()fxgxAB(3)()lim(0)()fxABgxB定理9数列的极限存在,则其子序列的极限一定存在且就等于该数列的极限．定理10初等函数在其定义域的区间内连续．定理11设fx连续,则fx也连续．（六）重要公式(重点记忆内容,应考必备)(1)0sinlim1xxx(2)101lim(1)e,lim(1)enxxnxn.(通过变量替换,这两个公式可写成...