大学物理学(上)第四版答案上海交大第一章

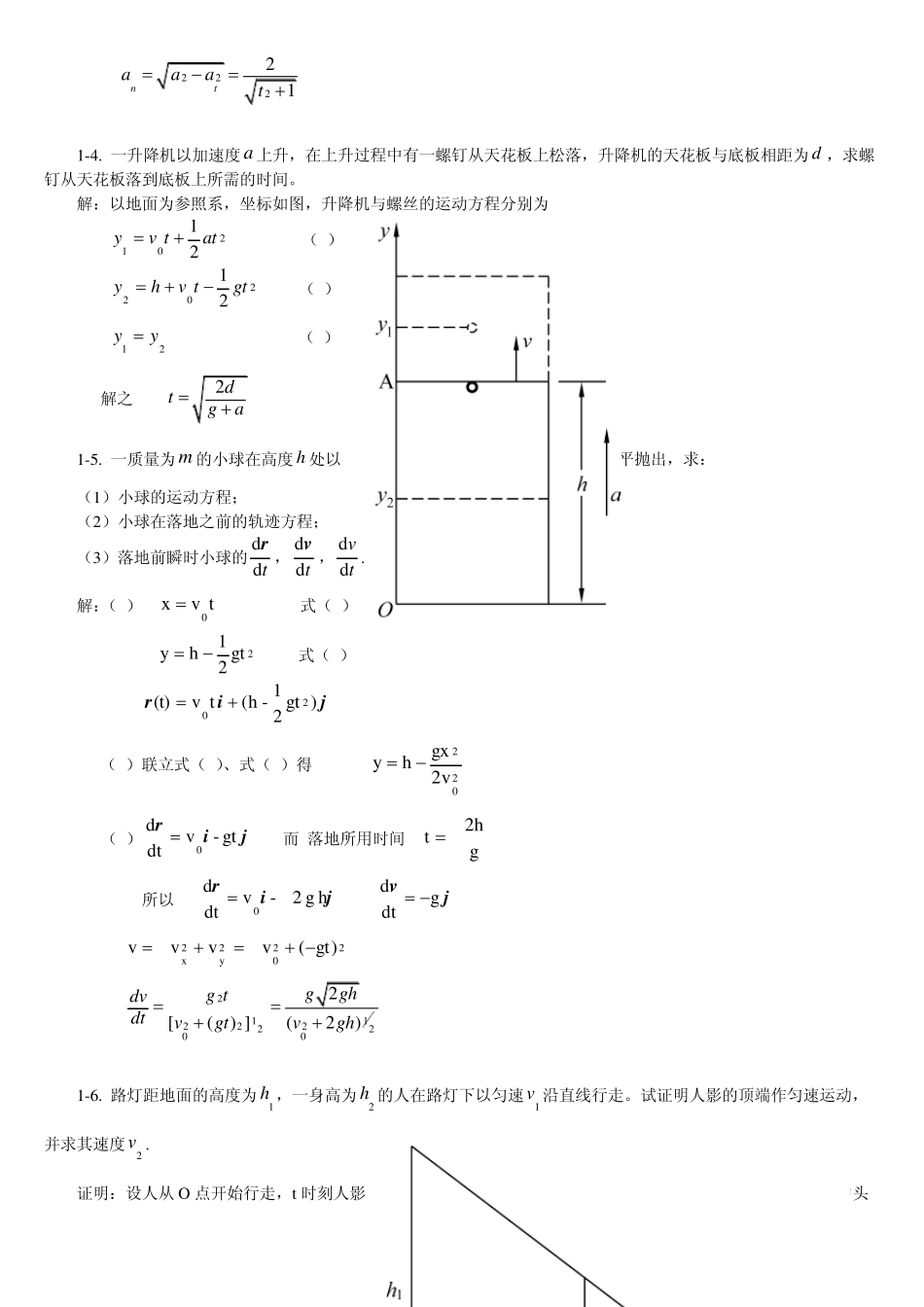
习 题 1-1. 已知质点位矢随时间变化的函数形式为 )ω tsinω t(cosji Rr 其中 为常量．求：（1）质点的轨道；(2)速度和速率。 解：1） 由)ω tsinω t(cosji  Rr知 tcosRxω tsinRyω 消去 t 可得轨道方程 222Ryx 2） jrvtRcossinωωtωRωdtdi RωtωRωtωRωv2122])c o s()s i n[( 1-2. 已知质点位矢随时间变化的函数形式为jir)t23(t4 2，式中r 的单位为m ，t 的单位为s .求：（1）质点的轨道；（2）从0t到1t秒的位移；（3）0t和1t秒两时刻的速度。 解：1）由jir)t23(t4 2可知 2t4x  t23y 消去 t 得轨道方程为：2)3y(x 2）jirv2t8dtd jijivr24)dt2t8(dt1010Δ 3） jv2(0)  jiv28( 1 ) 1-3. 已知质点位矢随时间变化的函数形式为jirtt22 ，式中r 的单位为m ，t 的单位为s .求：（1）任一时刻的速度和加速度；（2）任一时刻的切向加速度和法向加速度。 解：1）jirv2t2dtd iva2dtd 2）212212)1t(2]4)t2[(v 1tt2dtdva2t 22221ntaaat 1-4. 一升降机以加速度a 上升，在上升过程中有一螺钉从天花板上松落，升降机的天花板与底板相距为d ，求螺钉从天花板落到底板上所需的时间。 解：以地面为参照系，坐标如图，升降机与螺丝的运动方程分别为 20121 attvy （1） 图 1-4 20221 gttvhy （2） 21yy  （3） 解之 2dtga 初速度0v 水平抛出，求： 1-5. 一质量为m 的小球在高度h 处以（1）小球的运动方程； （2）小球在落地之前的轨迹方程； （3）落地前瞬时小球的tddr，tddv，tvdd. 解：（1） tvx0 式（1） 2gt21hy 式（2） jir)gt21-h(tv(t)20 （2）联立式（1）、式（2）得 202v2gxhy （3）jirgt-vtdd0 而 落地所用时间 gh2t  所以 jir2 g h-vtdd0 jvgtdd 2202y2x)gt(vvvv 21122222002[() ](2)gghg tdvdtvgtvgh 1-6. 路灯距地面的高度为1h ，一身高为2h 的人在路灯下以匀速1v 沿直线行走。试证明人影的顶端作匀速运动，并求其速度2v . 中足的坐标为1x ，人影中头证明：设人从O 点开始行走，t 时刻人影的坐标为2x ，由几何关系可得 图 1-6 21122hhxxx 而 tvx01  所以，人影中头的运动方程为 021121112vhhthhhxhx...