大学物理马文蔚第一章答案

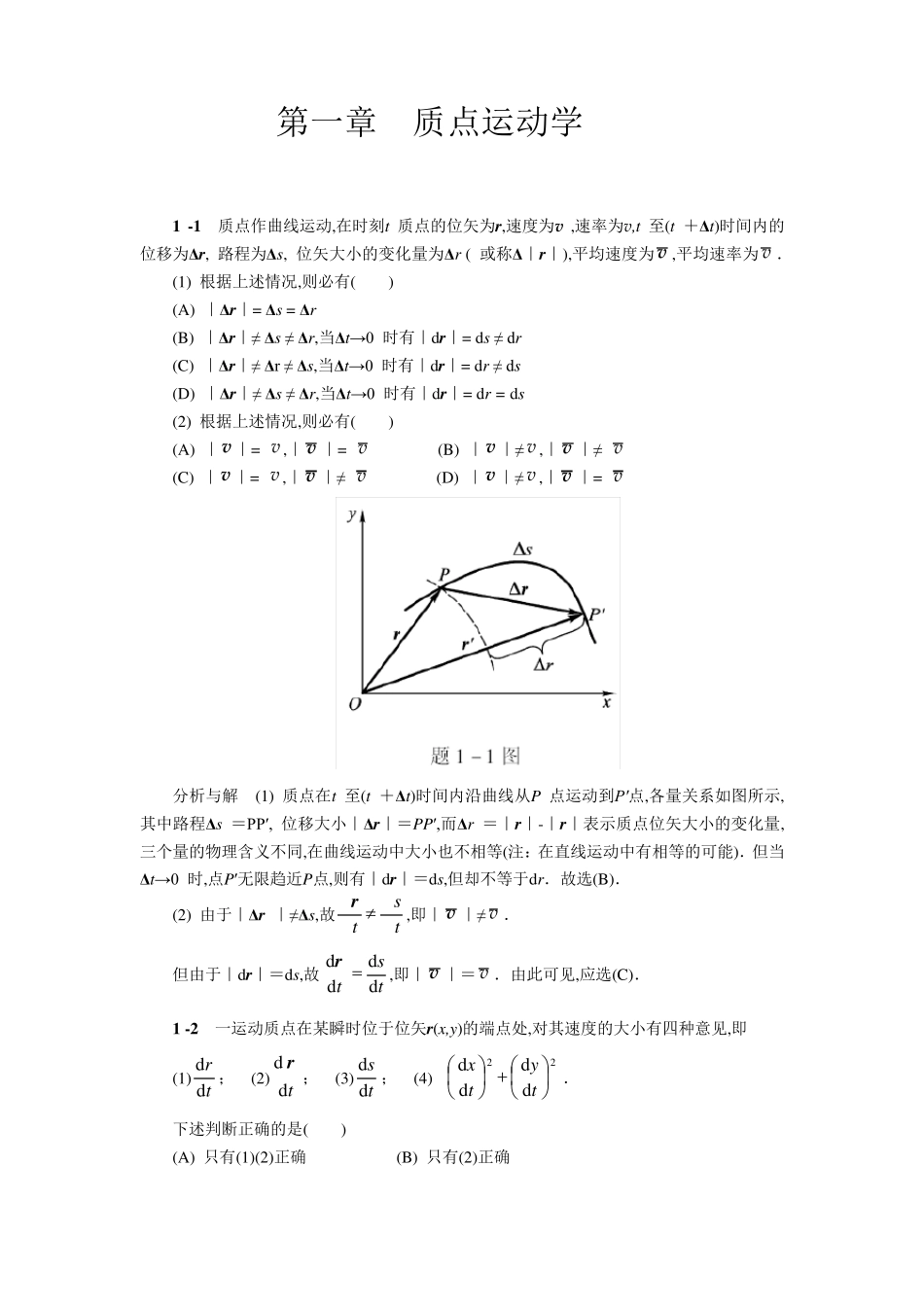
第一章 质点运动学 1 -1 质点作曲线运动,在时刻t 质点的位矢为r,速度为v ,速率为v,t 至(t ＋Δt)时间内的位移为Δr, 路程为Δs, 位矢大小的变化量为Δr ( 或称Δ｜r｜),平均速度为v ,平均速率为 v ． (1) 根据上述情况,则必有( ) (A) ｜Δr｜= Δs = Δr (B) ｜Δr｜≠ Δs ≠ Δr,当Δt→0 时有｜dr｜= ds ≠ dr (C) ｜Δr｜≠ Δr ≠ Δs,当Δt→0 时有｜dr｜= dr ≠ ds (D) ｜Δr｜≠ Δs ≠ Δr,当Δt→0 时有｜dr｜= dr = ds (2) 根据上述情况,则必有( ) (A) ｜v ｜= v ,｜v ｜= v (B) ｜v ｜≠ v ,｜v ｜≠ v (C) ｜v ｜= v ,｜v ｜≠ v (D) ｜v ｜≠ v ,｜v ｜= v 分析与解 (1) 质点在t 至(t ＋Δt)时间内沿曲线从P 点运动到P′点,各量关系如图所示, 其中路程Δs ＝PP′, 位移大小｜Δr｜＝PP′,而Δr ＝｜r｜-｜r｜表示质点位矢大小的变化量,三个量的物理含义不同,在曲线运动中大小也不相等(注：在直线运动中有相等的可能)．但当Δt→0 时,点P′无限趋近P点,则有｜dr｜＝ds,但却不等于dr．故选(B)． (2) 由于｜Δr ｜≠Δs,故tstΔΔΔΔ r,即｜v ｜≠ v ． 但由于｜dr｜＝ds,故tstdddd r,即｜v ｜＝ v ．由此可见,应选(C)． 1 -2 一运动质点在某瞬时位于位矢r(x ,y )的端点处,对其速度的大小有四种意见,即 (1) trdd； (2)tddr； (3) tsdd； (4)22ddddtytx． 下述判断正确的是( ) (A) 只有(1)(2)正确 (B) 只有(2)正确 (C) 只有(2)(3)正确 (D) 只有(3)(4)正确 分析与解 trdd表示质点到坐标原点的距离随时间的变化率,在极坐标系中叫径向速率．通常用符号vr表示,这是速度矢量在位矢方向上的一个分量；tddr表示速度矢量；在自然坐标系中速度大小可用公式tsddv计算,在直角坐标系中则可由公式22ddddtytxv求解．故选(D)． 1 -3 质点作曲线运动,r 表示位置矢量, v表示速度,a表示加速度,s 表示路程, aｔ表示切向加速度．对下列表达式,即 (1)d v /dt ＝a；(2)dr/dt ＝v；(3)ds/dt ＝v；(4)d v /dt｜＝aｔ． 下述判断正确的是( ) (A) 只有(1)、(4)是对的 (B) 只有(2)、(4)是对的 (C) 只有(2)是对的 (D) 只有(3)是对的 分析与解 tddv表示切向加速度aｔ,它表示速度大小随时间的变化率,是加速度矢量沿速度方向的一个分量,起...