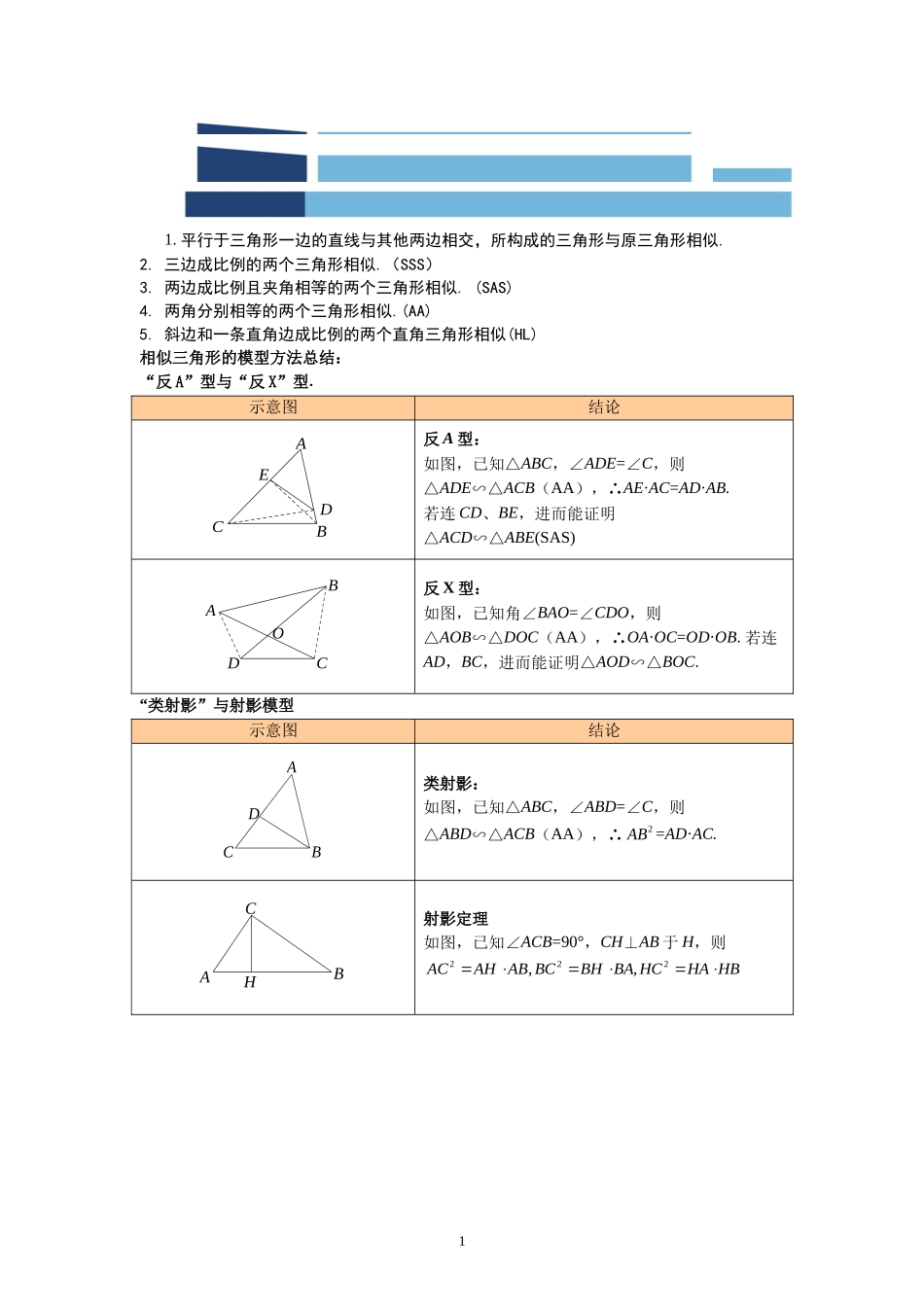
相似三角形的判定方法总结:1. 平行于三角形一边的直线与其他两边相交,所构成的三角形与原三角形相似.2. 三边成比例的两个三角形相似.(SSS)3. 两边成比例且夹角相等的两个三角形相似. (SAS)4. 两角分别相等的两个三角形相似.(AA)5. 斜边和一条直角边成比例的两个直角三角形相似(HL)相似三角形的模型方法总结:“反 A”型与“反 X”型.示意图结论EDCBA反 A 型:如图,已知△ABC,∠ADE=∠C,则△ADE∽△ACB(AA),∴AE·AC=AD·AB.若连 CD、BE,进而能证明△ACD∽△ABE(SAS)ODCBA反 X 型:如图,已知角∠BAO=∠CDO,则△AOB∽△DOC(AA),∴OA·OC=OD·OB. 若连AD,BC,进而能证明△AOD∽△BOC.“类射影”与射影模型示意图结论ABCD类射影:如图,已知△ABC,∠ABD=∠C,则△ABD∽△ACB(AA),∴2AB =AD·AC.CABH射影定理如图,已知∠ACB=90°,CH⊥AB 于 H,则222,,ACAH AB BCBH BA HCHA HB 1第 2 讲相似三角形 6 大证明技巧模块一相似三角形证明方法1“旋转相似”与“一线三等角”示意图结论ABCDE旋转相似:如图,已知△ABC∽△ADE,则ABADACAE ,∠BAC=∠DAE,∴∠BAD=∠CAE,∴△BAD∽△CAE(SAS)CBAED一线三等角:如图,已知∠A=∠C=∠DBE,则△DAB∽△BCE(AA) 巩固练习反 A 型与反 X 型已知△ABC 中,∠AEF=∠ACB,求证:(1)(2)∠BEO=∠CFO, ∠EBO=∠FCO(3)∠OEF=∠OBC,∠OFE=∠OCBOFECBA类射影如图,已知,求证:ABCD射影定理已知△ABC,∠ACB=90°,CH⊥AB 于 H,求证:,,2通过前面的学习,我们知道,比例线段的证明,离不开“平行线模型”(A 型,X 型,线束型),也离不开上述的 6 种“相似模型”. 但是,王老师认为,“模型”只是工具,怎样选择工具,怎样使用工具,怎样用好工具,取决于我们如何思考问题. 合理的思维方法,能让模型成为解题的利刃,让复杂的问题变简单。在本模块中,我们将学比例式的证明中,会经常用到的思维技巧.技巧一:三点定型法技巧二:等线段代换技巧三:等比代换技巧四:等积代换技巧五:证等量先证等比技巧六:几何计算【例1】 如图,平行四边形中,是延长线上的一点,交于,求证:.ABCFDE【例2】 如图,中,,为的中点,交的延长线于,交于.求证:CBAEDM【例3】 如图,在中,是斜边上的高,的平分线交于,交于.求证:. DBACFE3模块二比例式的证明方法技巧一:三点定型3悄悄地替换比例式中的某条线段…【例4】 如图,在...