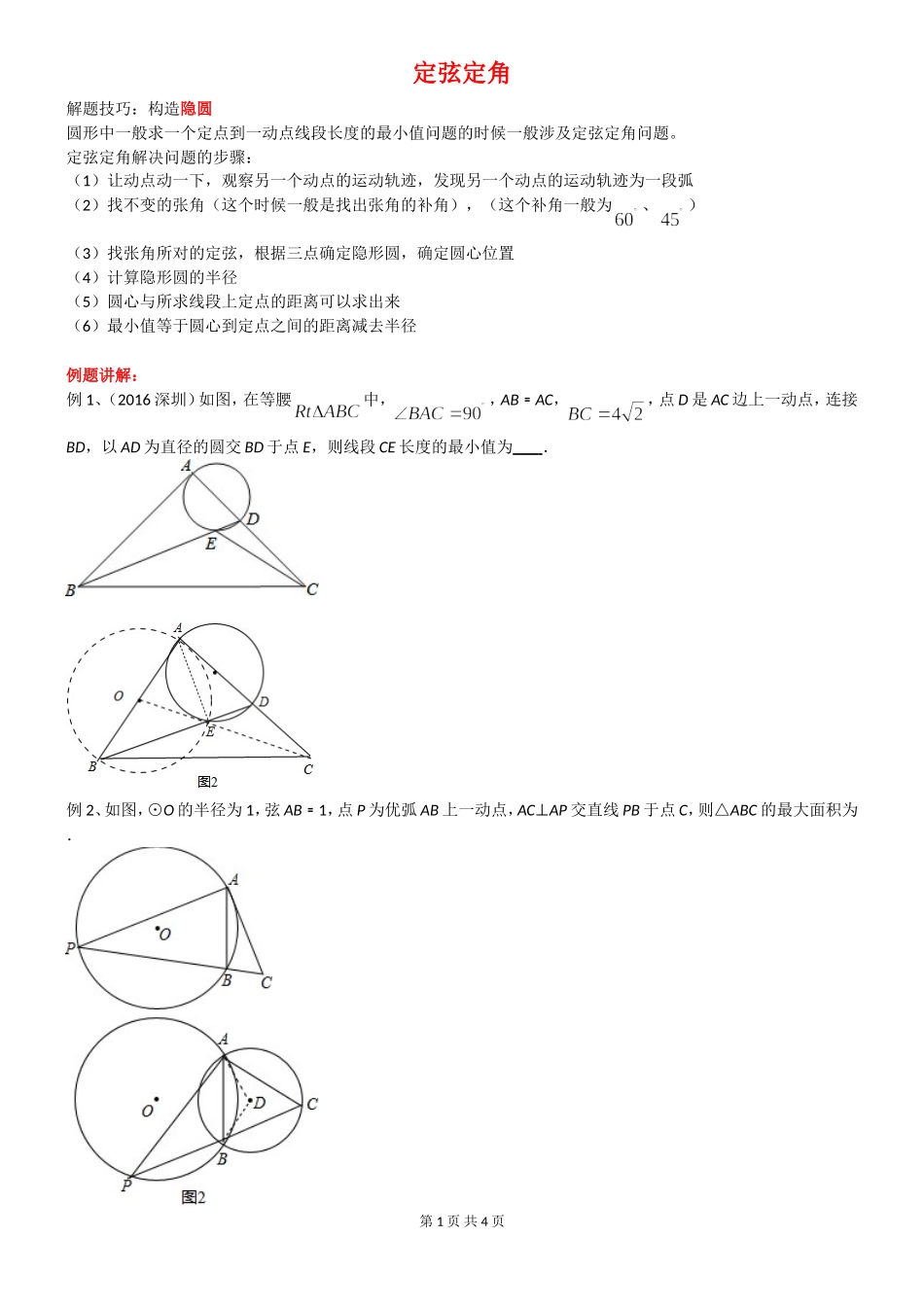
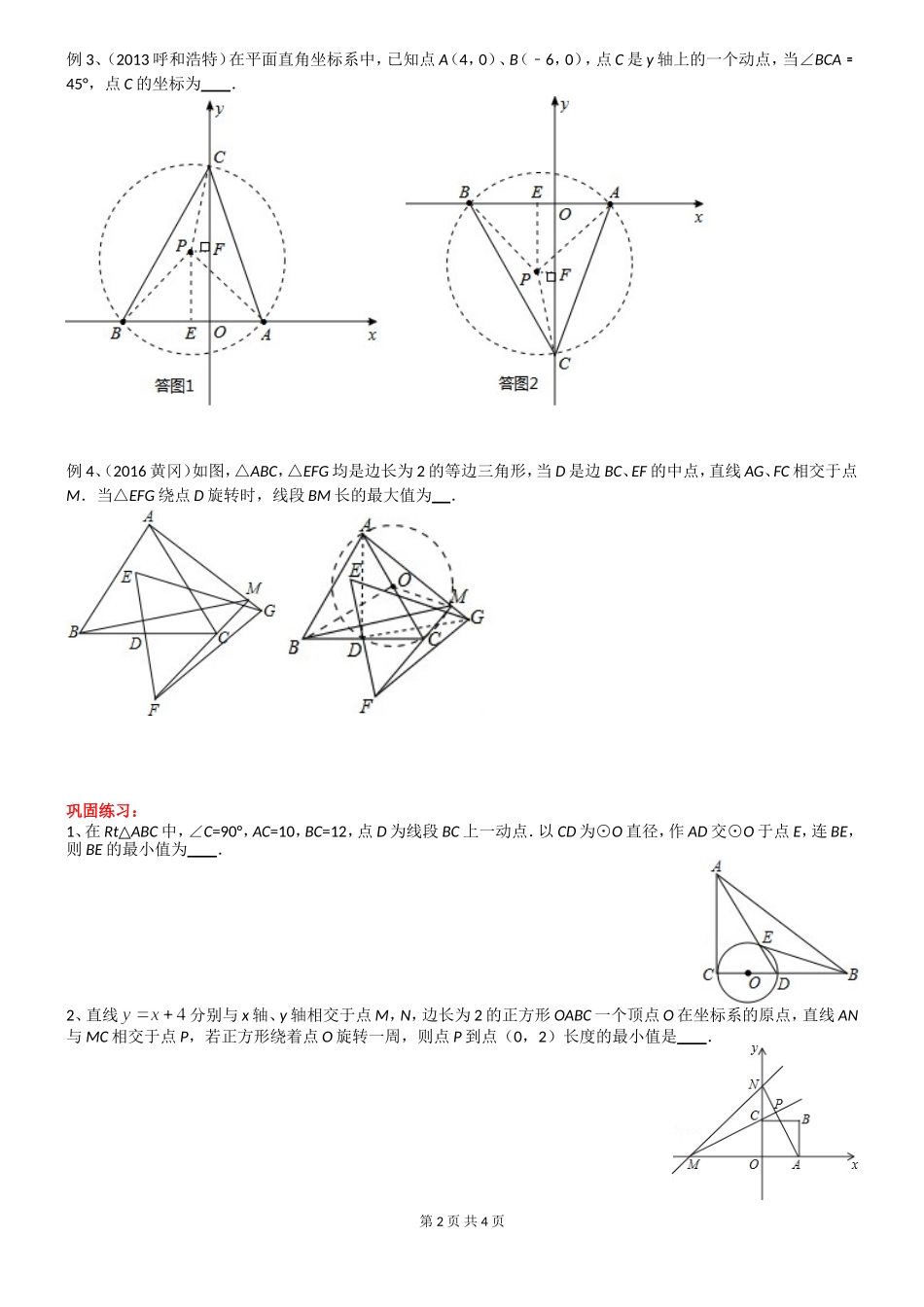
定弦定角解题技巧:构造隐圆圆形中一般求一个定点到一动点线段长度的最小值问题的时候一般涉及定弦定角问题。定弦定角解决问题的步骤:(1)让动点动一下,观察另一个动点的运动轨迹,发现另一个动点的运动轨迹为一段弧(2)找不变的张角(这个时候一般是找出张角的补角),(这个补角一般为、)(3)找张角所对的定弦,根据三点确定隐形圆,确定圆心位置(4)计算隐形圆的半径(5)圆心与所求线段上定点的距离可以求出来(6)最小值等于圆心到定点之间的距离减去半径例题讲解:例 1、(2016 深圳)如图,在等腰中,,AB﹦AC,,点 D 是 AC 边上一动点,连接BD,以 AD 为直径的圆交 BD 于点 E,则线段 CE 长度的最小值为 .例 2、如图,⊙O 的半径为 1,弦 AB﹦1,点 P 为优弧 AB 上一动点,AC⊥AP 交直线 PB 于点 C,则△ABC 的最大面积为 .第 1 页 共 4 页例 3、(2013 呼和浩特)在平面直角坐标系中,已知点 A(4,0)、B(﹣6,0),点 C 是 y 轴上的一个动点,当∠BCA﹦45°,点 C 的坐标为 .例 4、(2016 黄冈)如图,△ABC,△EFG 均是边长为 2 的等边三角形,当 D 是边 BC、EF 的中点,直线 AG、FC 相交于点M.当△EFG 绕点 D 旋转时,线段 BM 长的最大值为 .巩固练习:1、在 Rt△ABC 中,∠C=90°,AC=10,BC=12,点 D 为线段 BC 上一动点.以 CD 为⊙O 直径,作 AD 交⊙O 于点 E,连 BE,则 BE 的最小值为 .2、直线分别与 x 轴、y 轴相交于点 M,N,边长为 2 的正方形 OABC 一个顶点 O 在坐标系的原点,直线 AN与 MC 相交于点 P,若正方形绕着点 O 旋转一周,则点 P 到点(0,2)长度的最小值是 .第 2 页 共 4 页3、如图,E,F 是正方形 ABCD 的边 AD 上两个动点,满足 AE=DF.连接 CF 交 BD 于点 G,连接 BE 交 AG 于点 H.若正方形的边长为 2,则线段 DH 长度的最小值是 .4、如图,以 G(0,1)为圆心,半径为 2 的圆与 x 轴交于 A、B 两点,与 y 轴交于 C、D 两点,点 E 为⊙G 上一动点 ,CF⊥AE 于 F.若点 E 从在圆周上运动一周,则点 F 所经过的路径长为 .5、如图,△ABC 中,AC=3,BC=,∠ACB=45°,D 为△ABC 内一动点,⊙O 为△ACD 的外接圆,直线 BD 交⊙O 于 P 点,交 BC 于 E 点,弧 AE=CP,则 AD 的最小值为( )A.1B.2C.D.6、如图,...