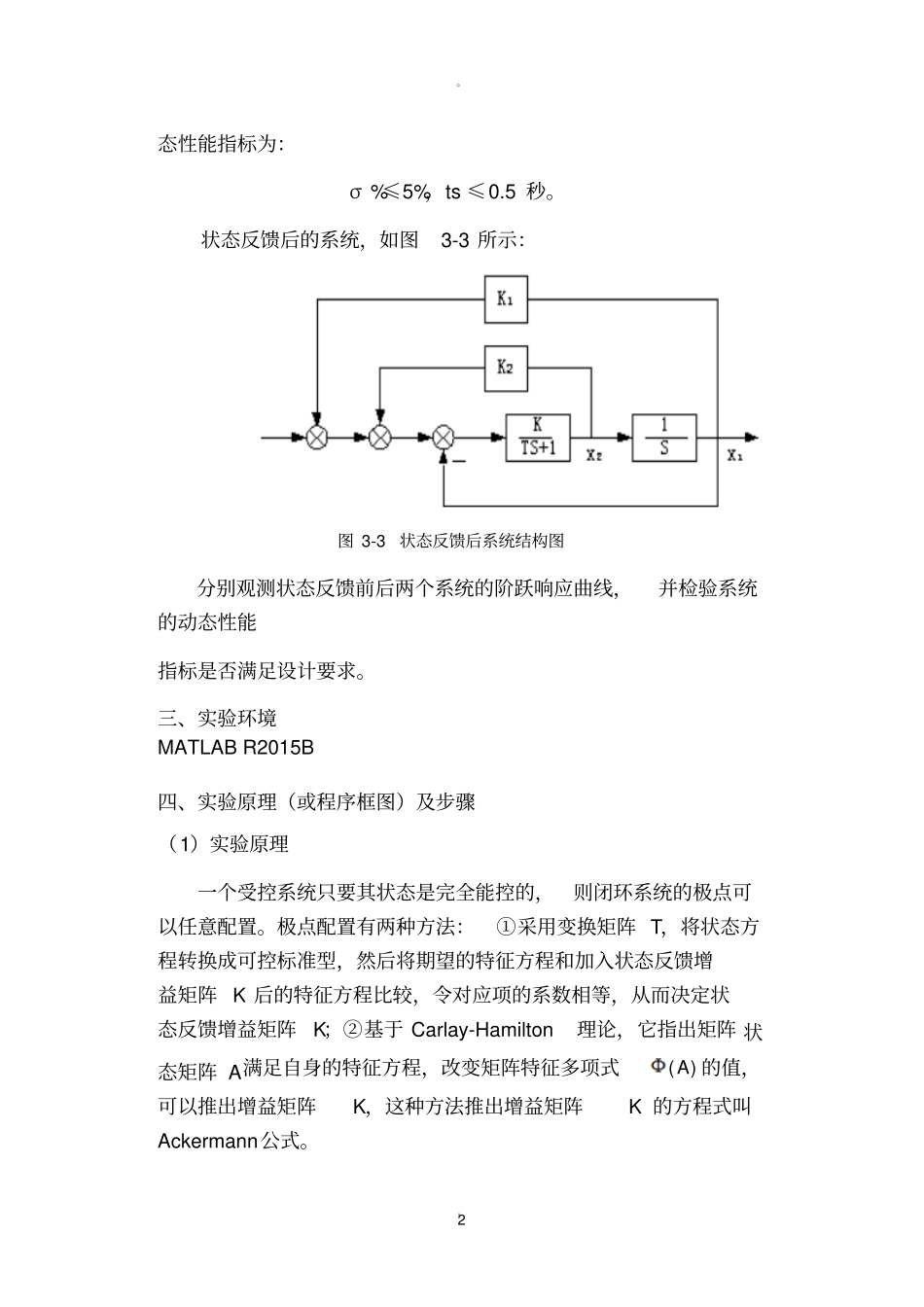
。。1 实 验 报 告课程线性系统理论基础实验日期 2016 年月日专业班级姓名学号同组人实验名称状态反馈极点配制方法的研究评分批阅教师签字一、实验目的1.掌握状态反馈系统的极点配置; 2.研究不同配置对系统动态特性的影响。二、实验内容原系统如图 3-2 所示。图中, X1和 X2 是可以测量的状态变量。图 3-2 系统结构图试设计状态反馈矩阵, 使系统加入状态反馈后其动态性能指标满足给定的要求: (1) 已知: K=10,T=1秒,要求加入状态反馈后系统的动态性能指标为:σ %≤20%,ts ≤1 秒。(12) 已知: K=1,T=0.05 秒,要求加入状态反馈后系统的动。。2 态性能指标为:σ %≤5%,ts ≤0.5 秒。状态反馈后的系统,如图3-3 所示:图 3-3 状态反馈后系统结构图分别观测状态反馈前后两个系统的阶跃响应曲线,并检验系统的动态性能指标是否满足设计要求。三、实验环境MATLAB R2015B 四、实验原理(或程序框图)及步骤(1)实验原理一个受控系统只要其状态是完全能控的,则闭环系统的极点可以任意配置。极点配置有两种方法:①采用变换矩阵 T,将状态方程转换成可控标准型,然后将期望的特征方程和加入状态反馈增益矩阵 K 后的特征方程比较,令对应项的系数相等,从而决定状态反馈增益矩阵K;②基于 Carlay-Hamilton理论,它指出矩阵 状态矩阵 A满足自身的特征方程,改变矩阵特征多项式)(A 的值,可以推出增益矩阵K,这种方法推出增益矩阵K 的方程式叫Ackermann公式。。。3 五、程序源代码(1)num=[10]; den=[1 1 10]; [A,B,C,D]=tf2ss(num,den); p=eig(A)' P=[-3+sqrt(-142)/2;-3-sqrt(-142)/2;] K=place(A,B,P) p=eig(A-B*K)' sysnew=ss(A-B*K,B,C,D) step(sysnew/dcgain(sysnew)) title('极点配置后系统阶跃响应') num=[10]; den=[1 1 10]; [A,B,C,D]=tf2ss(num,den); step(A,B,C,D) title('极点配置前系统的阶跃响应') (2) num=[1]; den=[1 1 0.5]; [A,B,C,D]=tf2ss(num,den); p=eig(A)' P=[-6+sqrt(-36);-6-sqrt(-36);] K=place(A,B,P) p=eig(A-B*K)' sysnew=ss(A-B*K,B,C,D) step(sysnew/dcgain(sysnew)) title('极点配置后系统的阶跃响应') num=[1]; den=[1 1 0.5]; [A,B,C,D]=tf2ss(num,den); >>step(A,B,C,D) >> title('极点配置前系统的阶跃响应') 六、实验数据、结果分析。。4 ( 1)p = -0.5000 - 3.1225i -0.5000 + 3.1225i P = -3.0000 +...