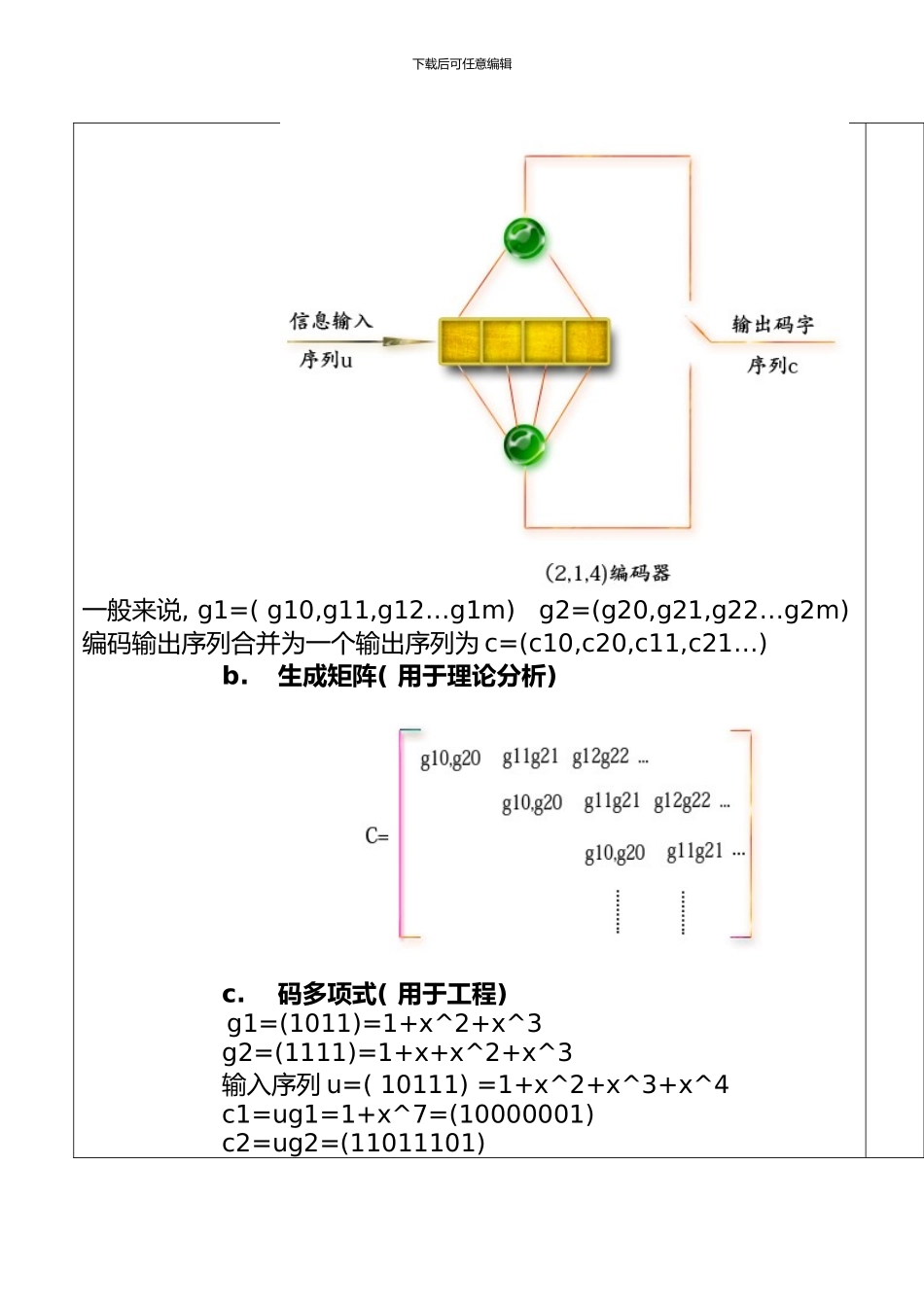
下载后可任意编辑下载后可任意编辑一.卷积码背景Elias 于 1955 年提出卷积码, 1967 年 Vterbi 提出最大似然译码法, 广泛运用于现代通信。二.编码原理1. 解析法a.离散卷积法( 用于定义) 包括: connection pictorial, connection vector, connection polynomial如下图: 设输入信息序列为 u=(u0,u1,u2……),对应输 c 出序列为( c10,c11,c12,c13…) ,c2=(c20,c21,c22,c23…),则编码方程可写为: c1=u*g1,c2=u*g2,c=(c1,c2),其中 g1,g2 表示编码器的两个脉冲冲激响应, 即编码可由输入信息序列 U 和编码器的两个冲激响应的卷积得到, 故如此称卷积码, 其中脉冲冲激响应应是指当输入为(1000…)时所观察到得两个输出序列值, 编码器m=3 级寄存器冲激响应可持续到 k=m+1=4 位。g1=( 1011) , g2=( 1111) 如下图: 下载后可任意编辑一般来说, g1=( g10,g11,g12…g1m) g2=(g20,g21,g22…g2m)编码输出序列合并为一个输出序列为 c=(c10,c20,c11,c21…)b.生成矩阵( 用于理论分析) c.码多项式( 用于工程) g1=(1011)=1+x^2+x^3g2=(1111)=1+x+x^2+x^3输入序列 u=( 10111) =1+x^2+x^3+x^4c1=ug1=1+x^7=(10000001)c2=ug2=(11011101)下载后可任意编辑2.卷积的图形表示法( state diagram, treediagram, trellis diagram) a.状态图: 编码器下一时刻的输出取决于取决于编码器当前状态及下一时刻输入, 而当前状态取决于各寄存器的存储状态内容, 因而总状态数达 2^mk个。如图: 状态表为: uiui-1si下载后可任意编辑00a10b01c11d有如下状态图: b.树图( 将状态图按时间展开) 设初始状态 s0=00 为树根, 对每个时刻的可能输入进行分支, 分数级数L 表示, L=0 时, u0=0 向上, u0=1 向下, 依次向后无限延伸, 分支上数字表示相应输出, a, b, c, d 表示状态。( 优点: 时序关系清楚) 下载后可任意编辑d.网格图( 讨论卷积码最大似然译码维特比算法的工具) 纵坐标表状态, 横坐标表时间。从图中我们可看出编码过程中使用 K-1 个冲洗比特使得编码器恢复初始状态是有必要的。下载后可任意编辑三、 卷积码的译码Viterbi 译码( 最大似然译码) 先验概率条件下, 后验概率最大者似然函数最大, 最值 MAP 即最大似然(ML)译码。而最大对数似然函数即计算最小汉明距, 如此, 比较接受序列和发送序列汉明距, 选出最小汉明距序列作为最佳译码即可。维特比译码思想: 译码过程选择整个集合路径...