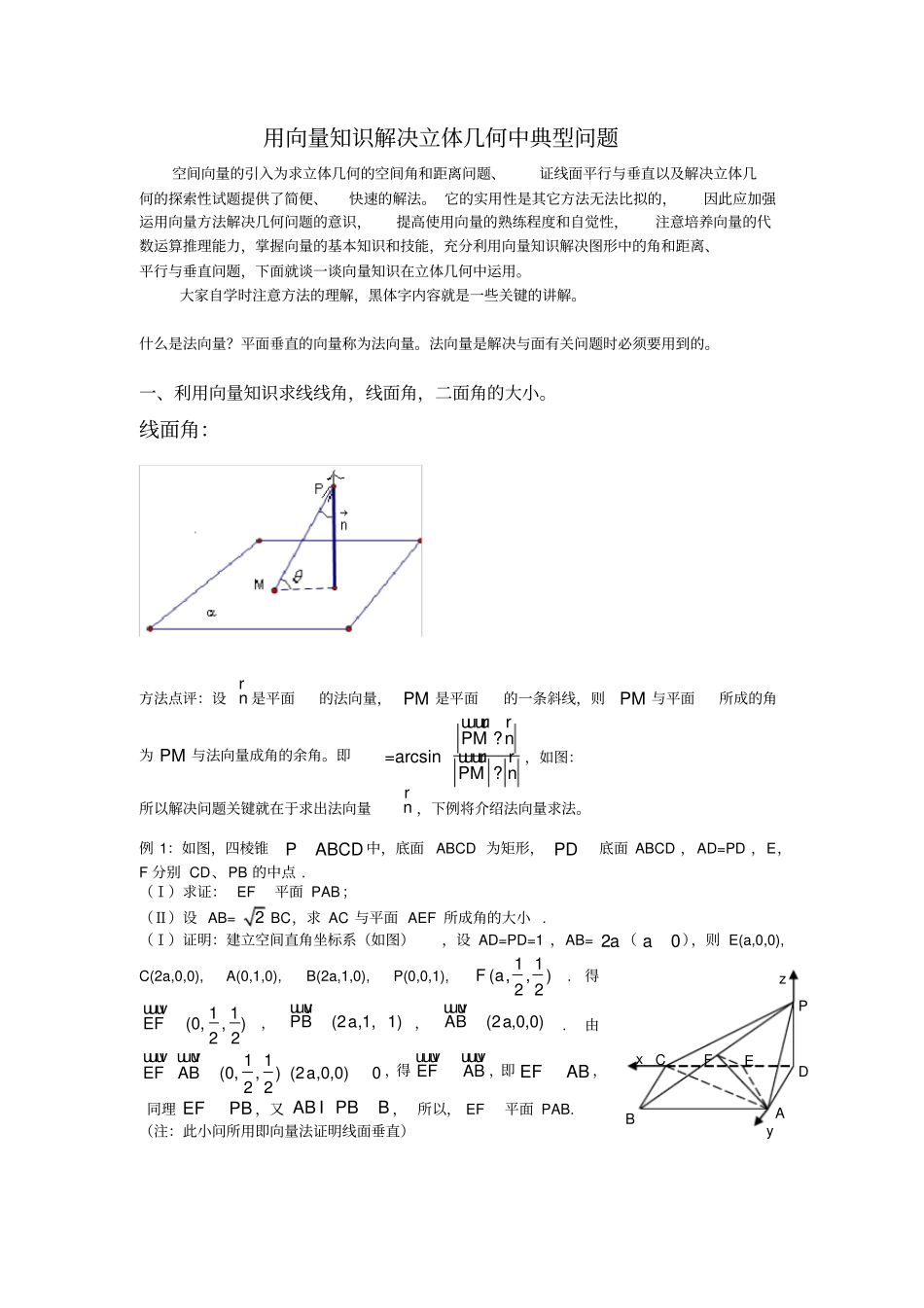
A B C D E F x y z P 用向量知识解决立体几何中典型问题空间向量的引入为求立体几何的空间角和距离问题、证线面平行与垂直以及解决立体几何的探索性试题提供了简便、快速的解法。 它的实用性是其它方法无法比拟的,因此应加强运用向量方法解决几何问题的意识,提高使用向量的熟练程度和自觉性,注意培养向量的代数运算推理能力,掌握向量的基本知识和技能,充分利用向量知识解决图形中的角和距离、平行与垂直问题,下面就谈一谈向量知识在立体几何中运用。大家自学时注意方法的理解,黑体字内容就是一些关键的讲解。什么是法向量?平面垂直的向量称为法向量。法向量是解决与面有关问题时必须要用到的。一、利用向量知识求线线角,线面角,二面角的大小。线面角:方法点评:设 nr是平面的法向量, PM 是平面的一条斜线,则PM 与平面所成的角为 PM 与法向量成角的余角。即PMnPMn??uuuurruuuurr=arcsin,如图:所以解决问题关键就在于求出法向量nr,下例将介绍法向量求法。例 1:如图,四棱锥PABCD 中,底面 ABCD 为矩形, PD底面 ABCD ,AD=PD ,E,F 分别 CD、PB 的中点 . (Ⅰ)求证: EF平面 PAB;(Ⅱ)设 AB=2 BC,求 AC 与平面 AEF 所成角的大小 . (Ⅰ)证明:建立空间直角坐标系(如图),设 AD=PD=1 ,AB= 2a (0a),则 E(a,0,0), C(2a,0,0), A(0,1,0), B(2a,1,0), P(0,0,1), 1 1( ,,)2 2F a.得1 1(0,,)2 2EFuuuv,(2 ,1, 1)PBauuuv,(2 ,0,0)ABauuuv. 由1 1(0,,) (2 ,0,0)02 2EFABauuuv uuuv,得 EFABuuuvuuuv,即 EFAB ,同理 EFPB ,又 ABPBBI, 所以, EF平面 PAB. (注:此小问所用即向量法证明线面垂直)ED1C1B1A1DCBA(Ⅱ)解:由2ABBC ,得 22a,即22a. 得2(,0,0)2E,2 1 1(,,)22 2F,(2,0,0)C. 有(2,1,0)ACuuuv,2(, 1,0)2AEuuuv,1 1(0,,)2 2EFuuuv. 设平面 AEF 的法向量为( , , )nx y zr,(如何来求这个法向量呢?注意到,既然要垂直平面,则要垂直平面内两相交直线,所以可以在平面内任意选择两条出来,然后分别和 nr做数量积, 利用数量积为0 建立两个等式, )由00n EFn AEruuuvruuuv1 1( , , ) (0,, )02 22( , , ) (, 1,0)02x y zx y z11022202yzxy,(两个条件肯定是求不出三个变量的,是因为平面的法向量不唯一,长度可以任意,但肯定都是和平面垂直的,所以我们只需要把其中一个数随意令成一个非...