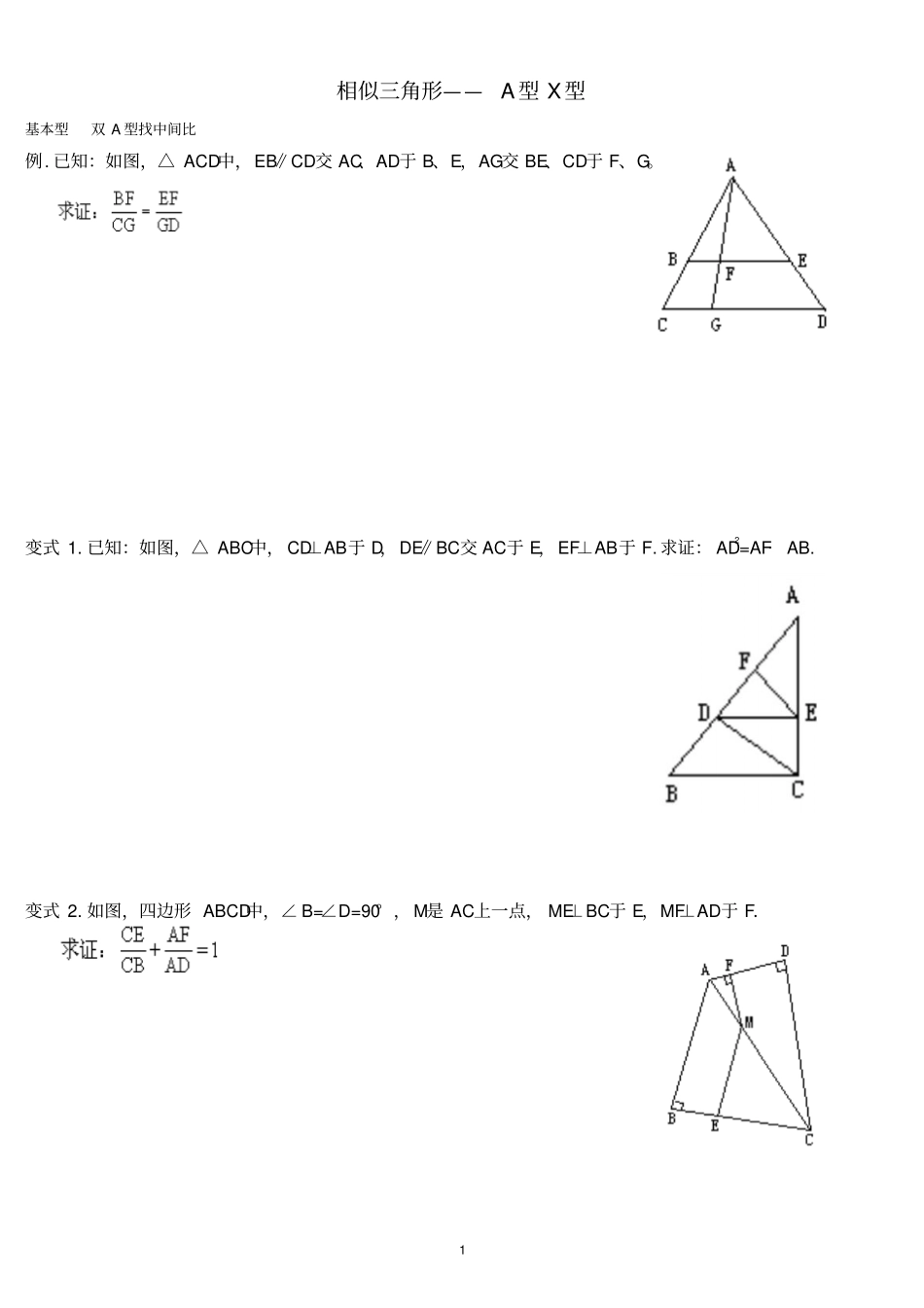
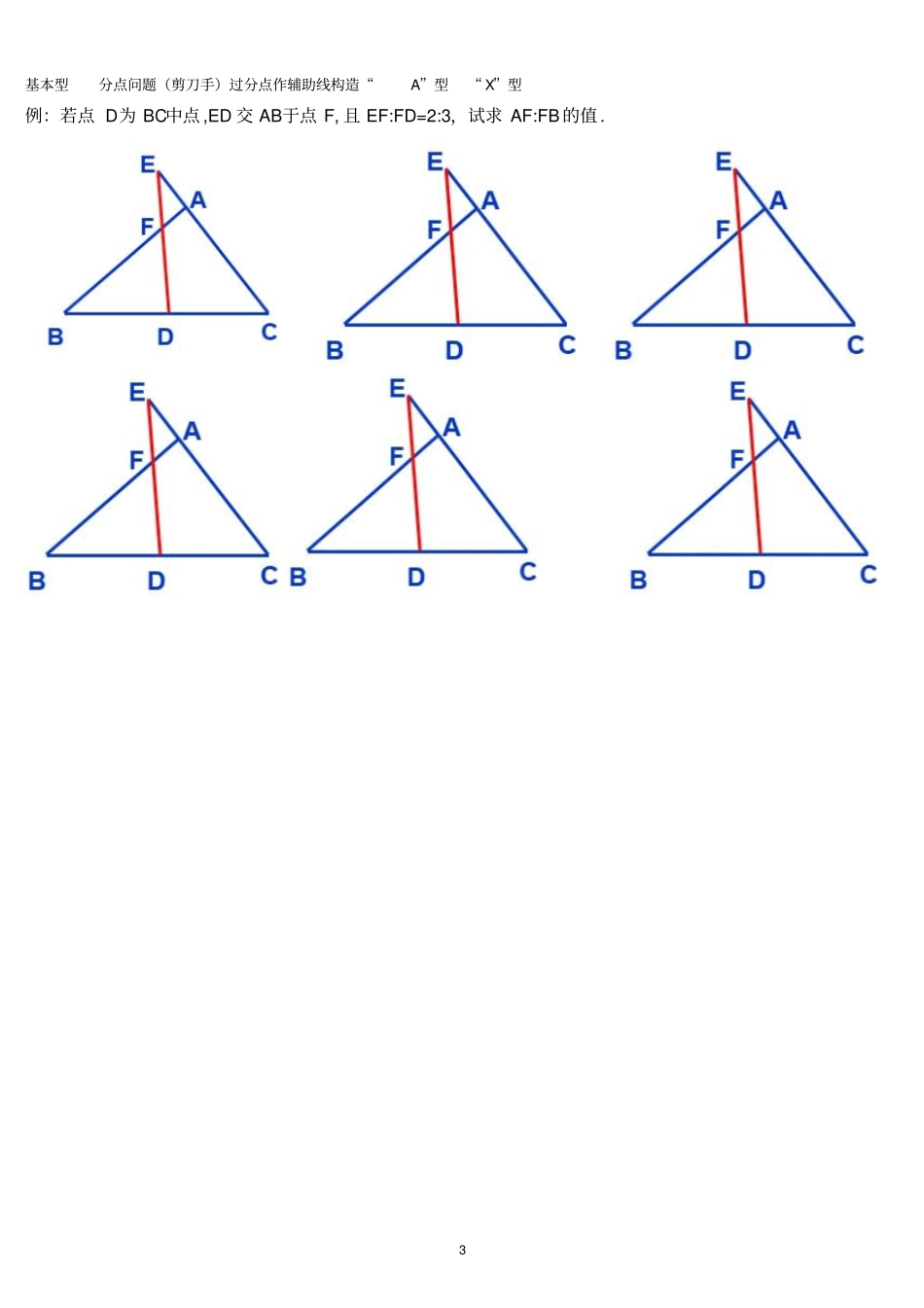
1 相似三角形——A 型 X 型基本型双 A 型找中间比例. 已知:如图,△ ACD中,EB∥CD交 AC、AD于 B、E,AG交 BE、CD于 F、G。变式 1. 已知:如图,△ ABC中, CD⊥AB于 D,DE∥BC交 AC于 E,EF⊥AB于 F. 求证: AD2=AF· AB. 变式 2. 如图,四边形 ABCD中,∠ B=∠D=90° , M是 AC上一点, ME⊥BC于 E,MF⊥AD于 F.2 基本型 A型 X 型找中间比例变式 1 变式 2: 如图, AD∥BC, O为对角线 AC、BD的交点,过 B作 BE∥CD交 CA延长线于 E。求证: OC2=OA· OE已知:平行四边形ABCD , E为 AB 的延长线上一点,连接 DE 交BC 于点 F, AB :BE=4 :3,求 CF :BC= ?已知: P为平行四边形ABCD 对角线 AC上一点,过点 P的直线与 AD 、BC ,CD 的延长线, AB 的延长线分别相交于点E、 F、 G、 H求证:PEPF =PHPG3 基本型分点问题(剪刀手)过分点作辅助线构造“A”型“ X”型例:若点 D为 BC中点 ,ED 交 AB于点 F, 且 EF:FD=2:3,试求 AF:FB 的值 . 4 变式 1:如图:过△ ABC的顶点 C作一条直线与中线AD和边 AB分别交于点 E和点 F , 且 AE:ED = 4:1 求:AF:FB 的值。变式 2:变式 3:已知:在ABC 中, D为 AB中点, E 为 AC上一点,且AEEC =2, BE 、 CD相交于点 F,求BFEF 的值已知:在ABC 中, AD=13 AB ,延长 BC到 F,使 CF=13 BC ,连接 FD交 AC于点 E,求证:( 1)DE=EF ,( 2) AE=2CE