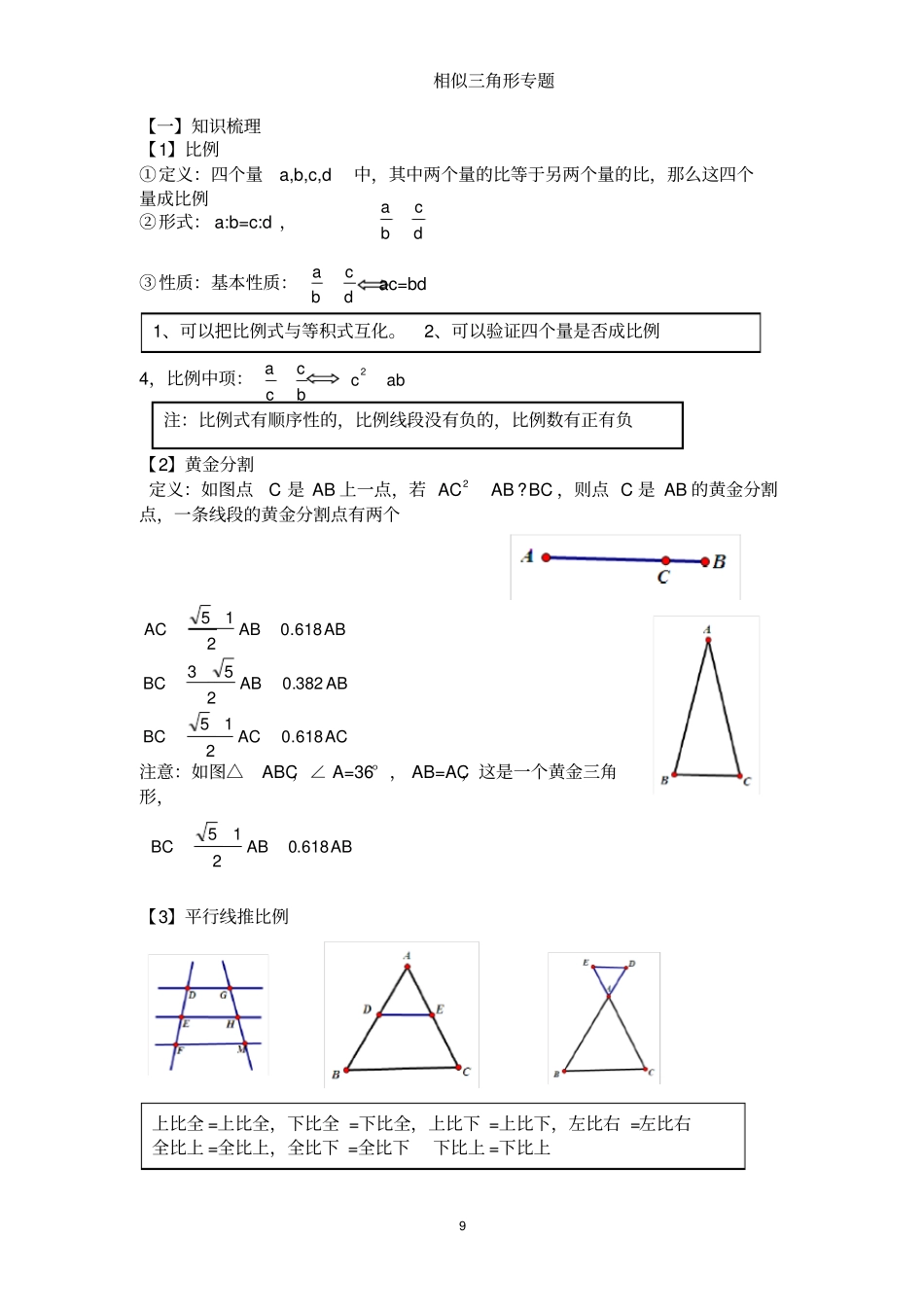
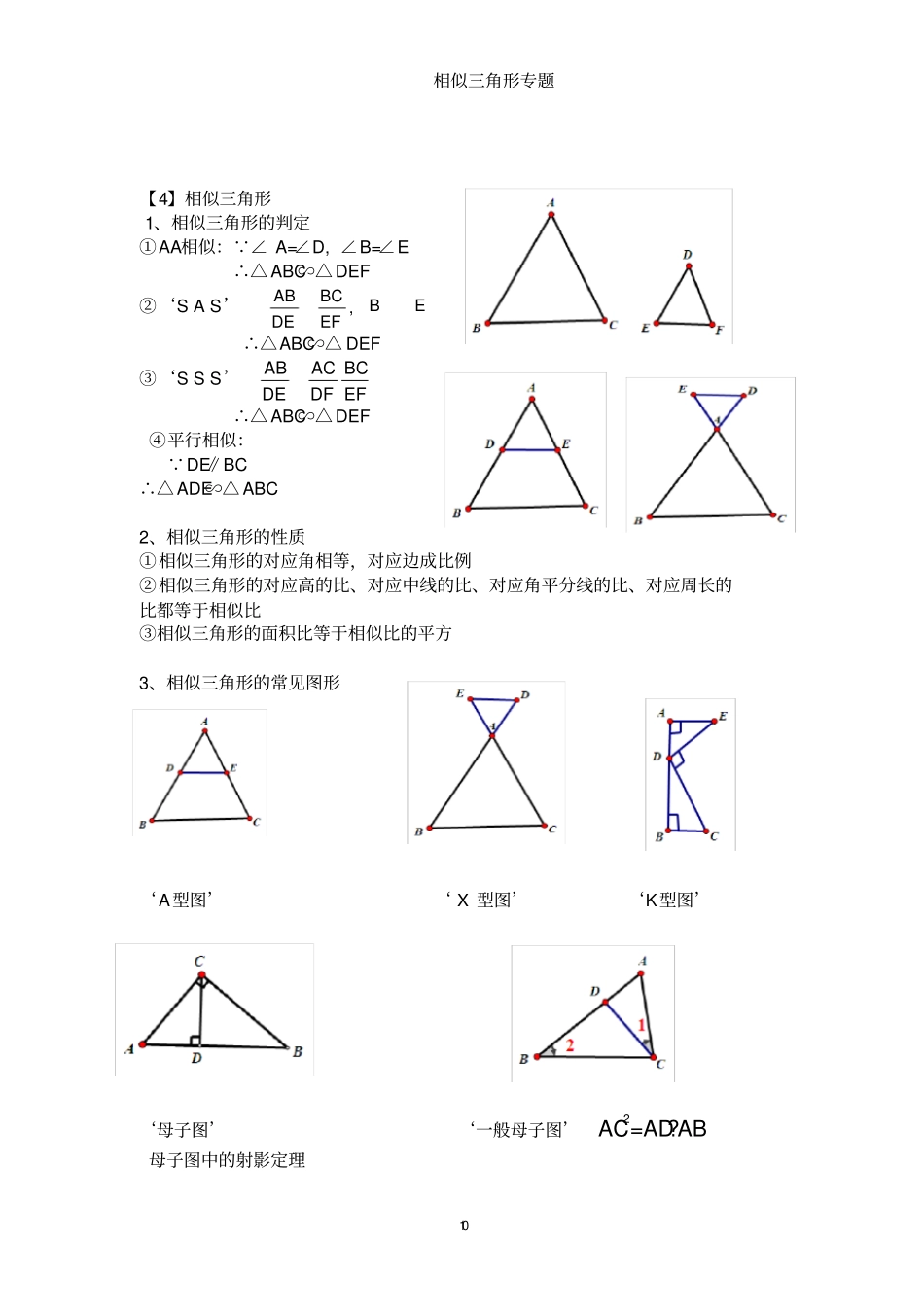
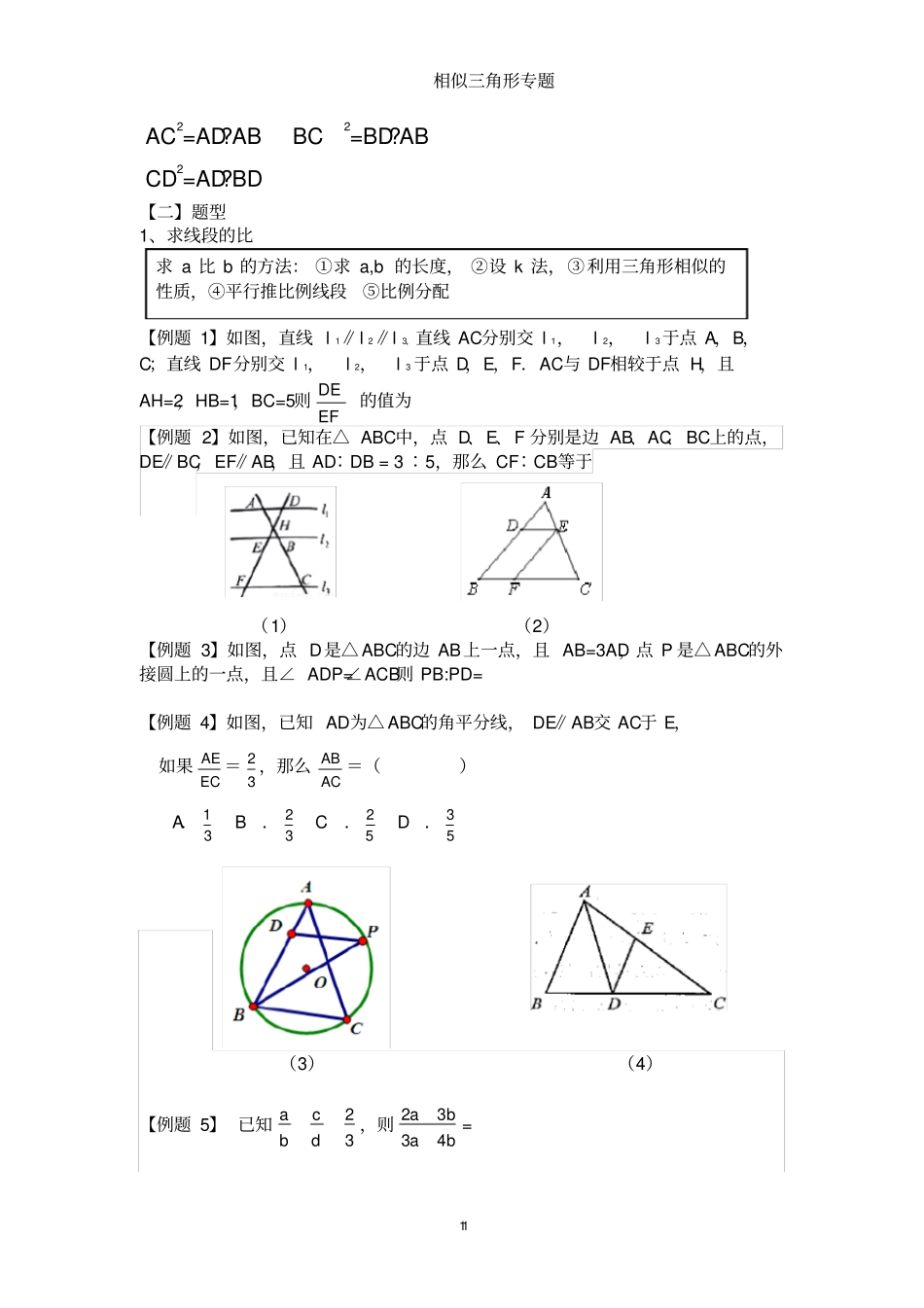
相似三角形专题9 【一】知识梳理【1】比例①定义:四个量a,b,c,d中,其中两个量的比等于另两个量的比,那么这四个量成比例②形式: a:b=c:d ,③性质:基本性质:dcba ac=bd 4,比例中项:bccaabc2【2】黄金分割定义:如图点C 是 AB 上一点,若BCABAC?2,则点 C 是 AB 的黄金分割点,一条线段的黄金分割点有两个ACACBCABABBCABABAC618.0215382.0253618.0215注意:如图△ABC,∠ A=36° , AB=AC,这是一个黄金三角形,【3】平行线推比例ABABBC618.0215dcba注:比例式有顺序性的,比例线段没有负的,比例数有正有负1、可以把比例式与等积式互化。2、可以验证四个量是否成比例上比全 =上比全,下比全 =下比全,上比下 =上比下,左比右 =左比右全比上 =全比上,全比下 =全比下下比上 =下比上相似三角形专题10【4】相似三角形1、相似三角形的判定①AA相似: ∠ A=∠D, ∠B=∠E ∴△ ABC∽△ DEF ②‘S A S’EBEFBCDEAB,∴△ABC∽△ DEF ③‘S S S’EFBCDFACDEAB∴△ ABC∽△ DEF ④平行相似: DE∥BC ∴△ ADE∽△ ABC 2、相似三角形的性质①相似三角形的对应角相等,对应边成比例②相似三角形的对应高的比、对应中线的比、对应角平分线的比、对应周长的比都等于相似比③相似三角形的面积比等于相似比的平方3、相似三角形的常见图形‘A型图’‘ X 型图’‘K型图’‘母子图’‘一般母子图’AC2=AD?AB 母子图中的射影定理相似三角形专题11 AC2=AD?AB BC2=BD?AB CD2=AD?BD 【二】题型1、求线段的比【例题 1】如图,直线 l 1∥l 2∥l 3,直线 AC分别交 l 1,l 2,l 3于点 A,B,C;直线 DF分别交 l 1,l 2,l 3 于点 D,E,F.AC与 DF相较于点 H,且AH=2,HB=1,BC=5则EFDE的值为【例题 2】如图,已知在△ ABC中,点 D、E、F 分别是边 AB、AC、 BC上的点,DE∥BC,EF∥AB,且 AD∶DB = 3 ∶5,那么 CF∶CB等于(1)(2)【例题 3】如图,点 D是△ ABC的边 AB上一点,且 AB=3AD,点 P 是△ ABC的外接圆上的一点,且∠ ADP=∠ACB则 PB:PD= 【例题 4】如图,已知 AD为△ ABC的角平分线, DE∥AB交 AC于 E,如果 AEEC= 23,那么 ABAC=()A. 13 B. 23 C. 25 D. 35(3)(4)【例题 5】 已知32dcba,则baba4332= 求 a 比 b 的方法: ①求 a,b 的长度, ②设 k 法,③利用三角形相似的性质,④平行推比例线段⑤比例分配相似三...