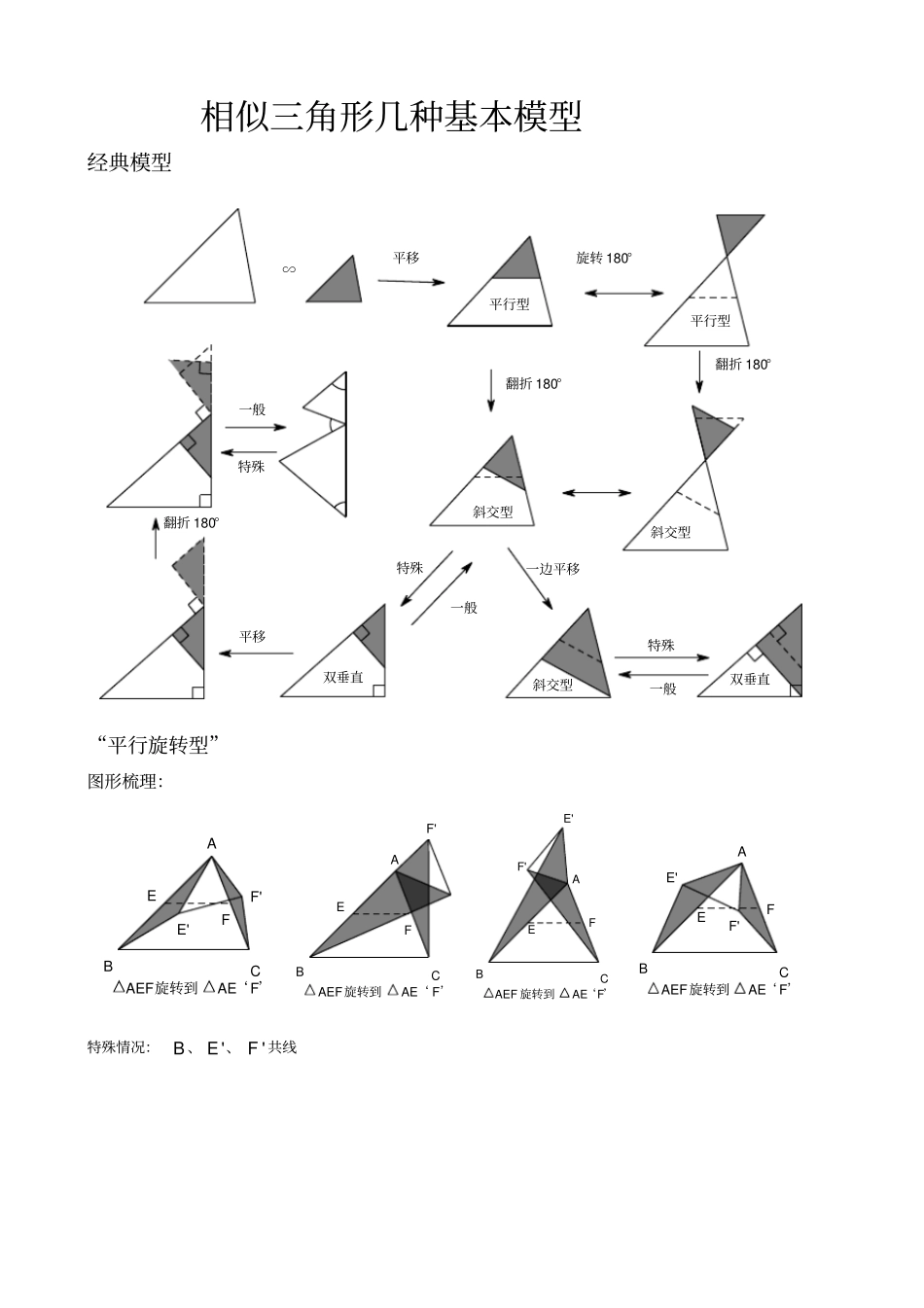
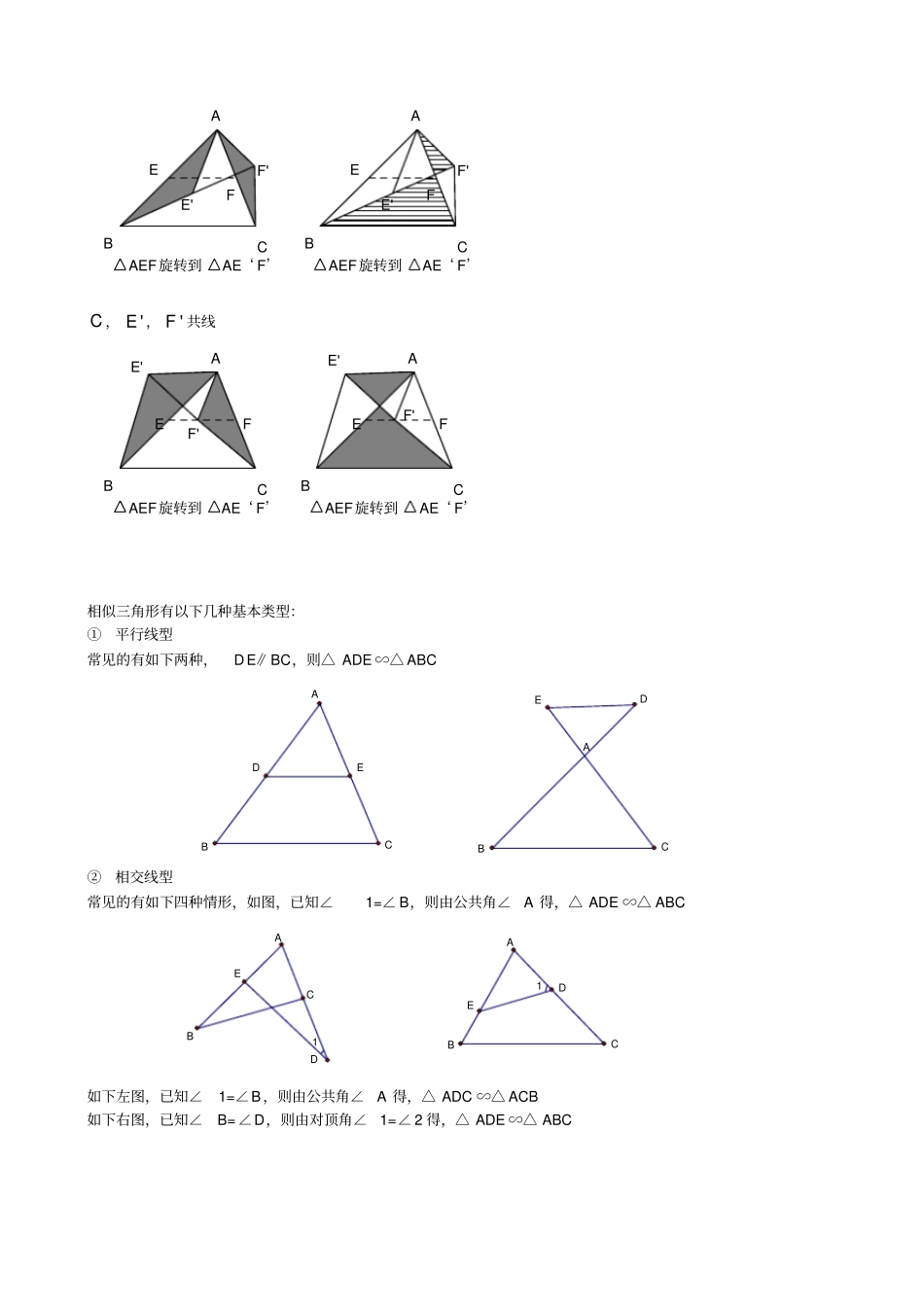
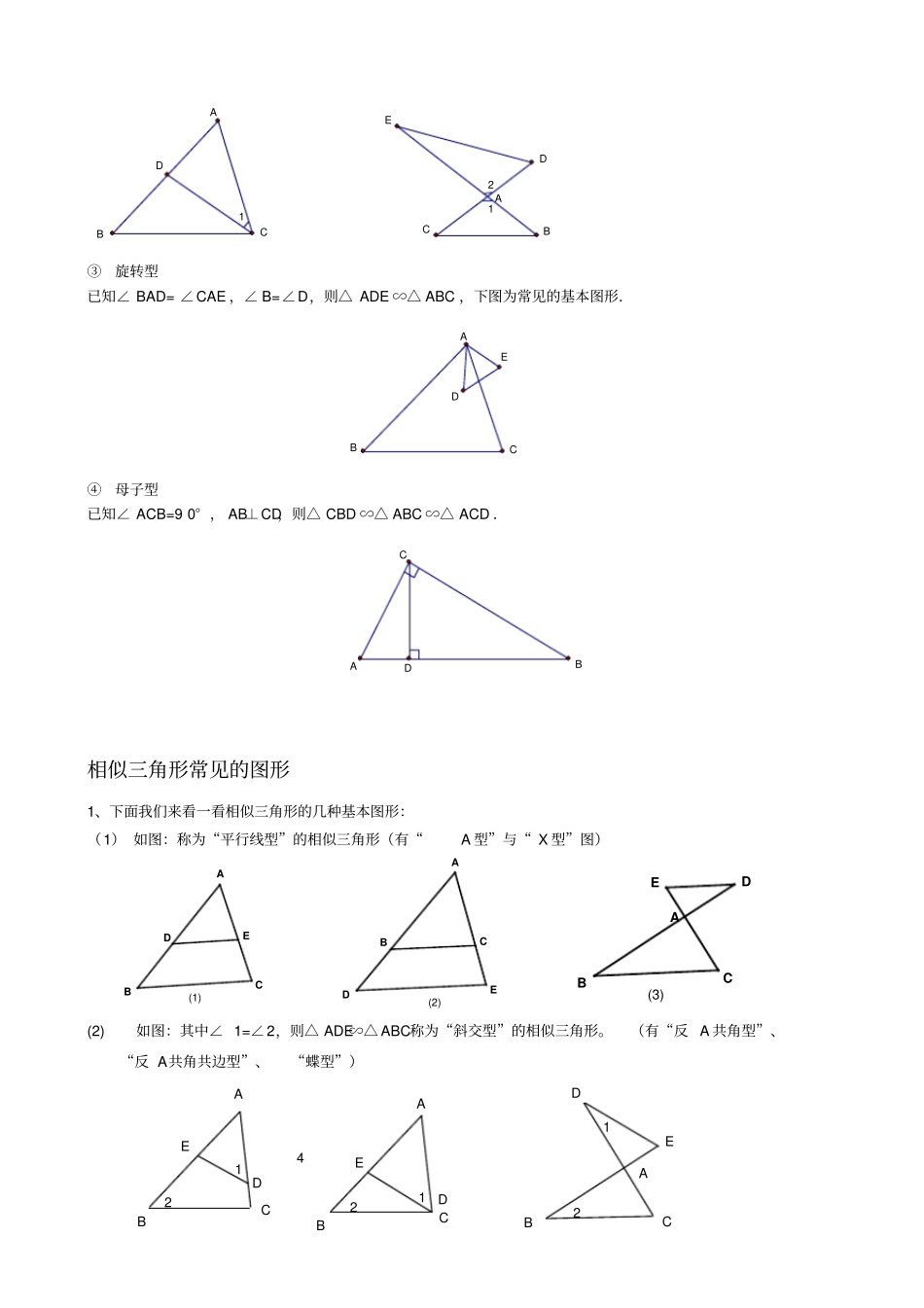
相似三角形几种基本模型经典模型特殊一般翻折 180°平移特殊一般一般翻折 180°双垂直双垂直斜交型斜交型斜交型平行型平行型特殊一边平移翻折 180°旋转 180°平移∽“平行旋转型”图形梳理:AEF旋转到AE‘F’F'E'FECBAAEF旋转到AE‘ F’F'FECBAABCEFE'F'AEF 旋转到AE‘F’ABCEFE'F'AEF旋转到AE‘F’特殊情况: B 、'E 、'F 共线AEF旋转到AE‘ F’F'E'FECBAABCEFE'F'AEF旋转到AE‘ F’C ,'E ,'F 共线AEF旋转到AE‘ F’F'E'FECBAAEF旋转到AE‘ F’F'E'FECBA相似三角形有以下几种基本类型:①平行线型常见的有如下两种,DE∥BC,则△ ADE ∽△ ABC AABCBCDEDE②相交线型常见的有如下四种情形,如图,已知∠1=∠ B,则由公共角∠A 得,△ ADE ∽△ ABC 11ABCDABCEED如下左图,已知∠1=∠B,则由公共角∠A 得,△ ADC ∽△ ACB 如下右图,已知∠B=∠D,则由对顶角∠1=∠ 2 得,△ ADE ∽△ ABC A211BCACBEDD③旋转型已知∠ BAD= ∠CAE ,∠ B=∠D,则△ ADE ∽△ ABC ,下图为常见的基本图形.BCADE④母子型已知∠ ACB=9 0° , AB⊥CD,则△ CBD ∽△ ABC ∽△ ACD .ABCD相似三角形常见的图形1、下面我们来看一看相似三角形的几种基本图形:(1) 如图:称为“平行线型”的相似三角形(有“A 型”与“ X 型”图)(2) 如图:其中∠ 1=∠2,则△ ADE∽△ ABC称为“斜交型”的相似三角形。(有“反 A 共角型”、“反 A共角共边型”、“蝶型”)ABCDE12AABBCCDDEE12412(1)EABCD(3)DBCAE(2)CDEAB(3)如图:称为“垂直型” (有“双垂直共角型” 、“双垂直共角共边型(也称“射影定理型”)”“三垂直型”)(4) 如图:∠ 1=∠2,∠B=∠D,则△ ADE∽△ ABC,称为“旋转型”的相似三角形。2、几种基本图形的具体应用:(1)若 DE∥BC( A型和 X 型)则△ ADE∽△ ABC (2)射影定理若 CD为 Rt△ABC斜边上的高(双直角图形)则 Rt△ABC∽Rt△ACD∽Rt△CBD且 AC2=AD·AB,CD2=AD·BD,BC2=BD·AB;EADCBEADCBADCB(3)满足 1、AC2=AD·AB,2、∠ ACD=∠B,3、∠ ACB=∠ADC,都可判定△ ADC∽△ ACB.(4)当 ADAEACAB或 AD· AB=AC·AE时,△ ADE∽△ ACB.ADCBEADCBBEACD12ECABDEABC(D)EADCB