相似三角形的知识点

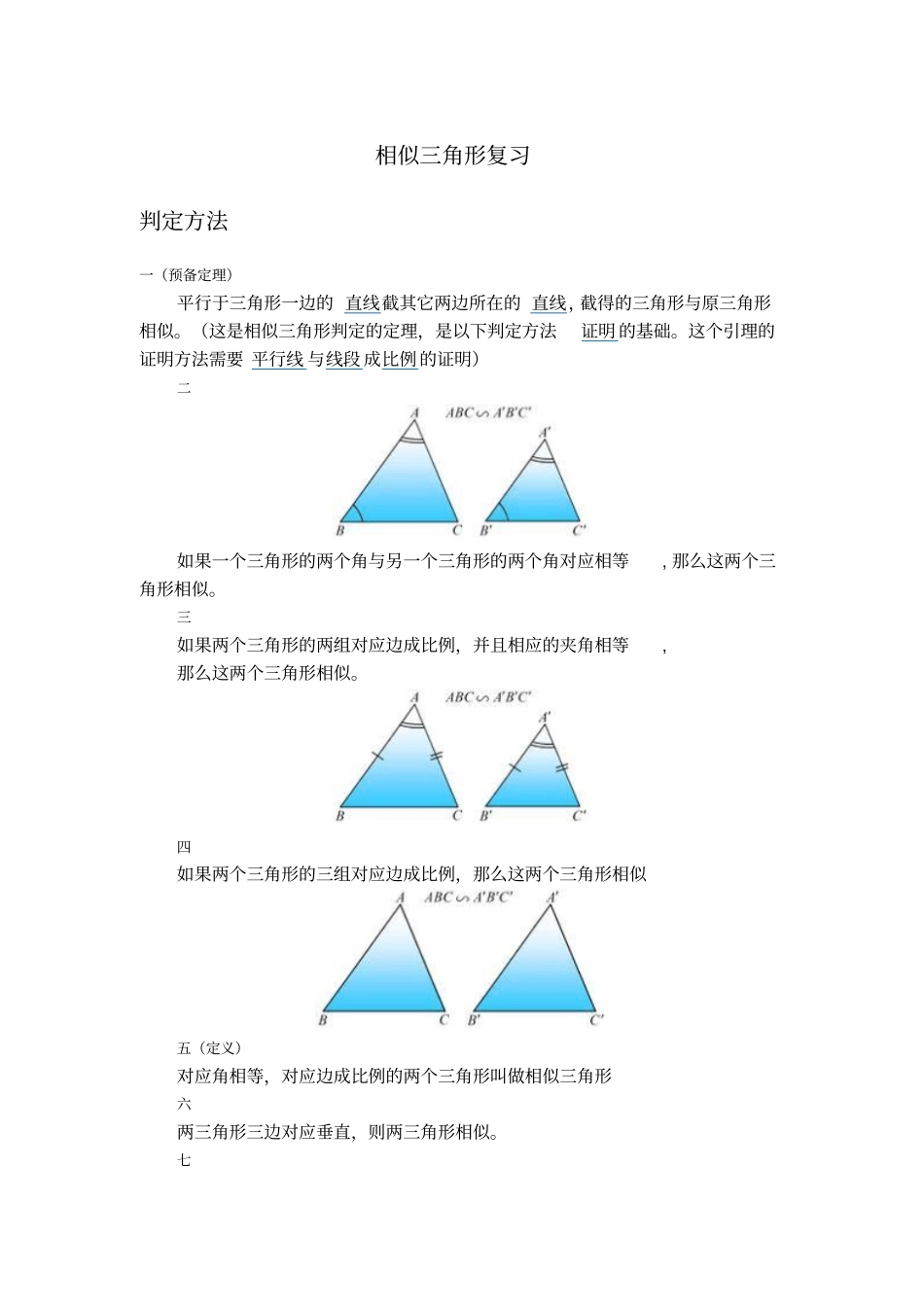
相似三角形复习判定方法一（预备定理）平行于三角形一边的 直线截其它两边所在的 直线，截得的三角形与原三角形相似。（这是相似三角形判定的定理，是以下判定方法证明 的基础。这个引理的证明方法需要 平行线 与线段 成比例 的证明）二如果一个三角形的两个角与另一个三角形的两个角对应相等, 那么这两个三角形相似。三如果两个三角形的两组对应边成比例，并且相应的夹角相等, 那么这两个三角形相似。四如果两个三角形的三组对应边成比例，那么这两个三角形相似五（定义）对应角相等，对应边成比例的两个三角形叫做相似三角形六两三角形三边对应垂直，则两三角形相似。七两个直角三角形中，斜边与直角边对应成比例，那么两三角形相似。八由角度比转化为线段比： h1/h2=Sabc 九（易失误）比值是一个具体的数字如：AB/EF=2 而比不是一个具体的数字如：AB/EF=2：1 2 一定相似1. 两个全等的三角形全等三角形 是特殊的相似三角形，相似比为1：1 2. 任意一个顶角或底角相等的两个等腰三角形两个 等腰三角形 ，如果其中的任意一个顶角或底角相等，那么这两个等腰三角形相似。3. 两个等边三角形( 两个等边三角形 ，三个内角都是 60 度，且边边相等，所以 相似 )4. 直角三角形中由斜边的高形成的三个三角形3 判定定理基本判定(1) 平行于三角形一边的直线和其他两边相交，所构成的三角形与原三角形相似。(2) 如果一个三角形的两条边和另一个三角形的两条边对应成比例，并且夹角相等，那么这两个三角形相似。( 简叙为：两边对应成比例且夹角相等，两个三角形相似。 ) (3) 如果一个三角形的三条边与另一个三角形的三条边对应成比例，那么这两个三角形相似。 ( 简叙为：三边对应成比例，两个三角形相似。) (4) 如果两个三角形的两个角分别对应相等（或三个角分别对应相等），那么这两个三角形相似。直角三角形判定(1) 直角三角形被斜边上的高分成两个直角三角形和原三角形相似。(2) 如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例，那么这两个直角三角形相似。性质定理(1) 相似三角形的对应角相等。(2) 相似三角形的对应边成比例。(3) 相似三角形的对应高线的比，对应中线的比和对应角平分线的比都等于相似比 。(4) 相似三角形的周长比等于相似比。(5) 相似三角形的面积比等于相似比的平方。4 定理推论推论一： 顶角 或底角相等的两个等腰三角形相似。推论二：腰和底...