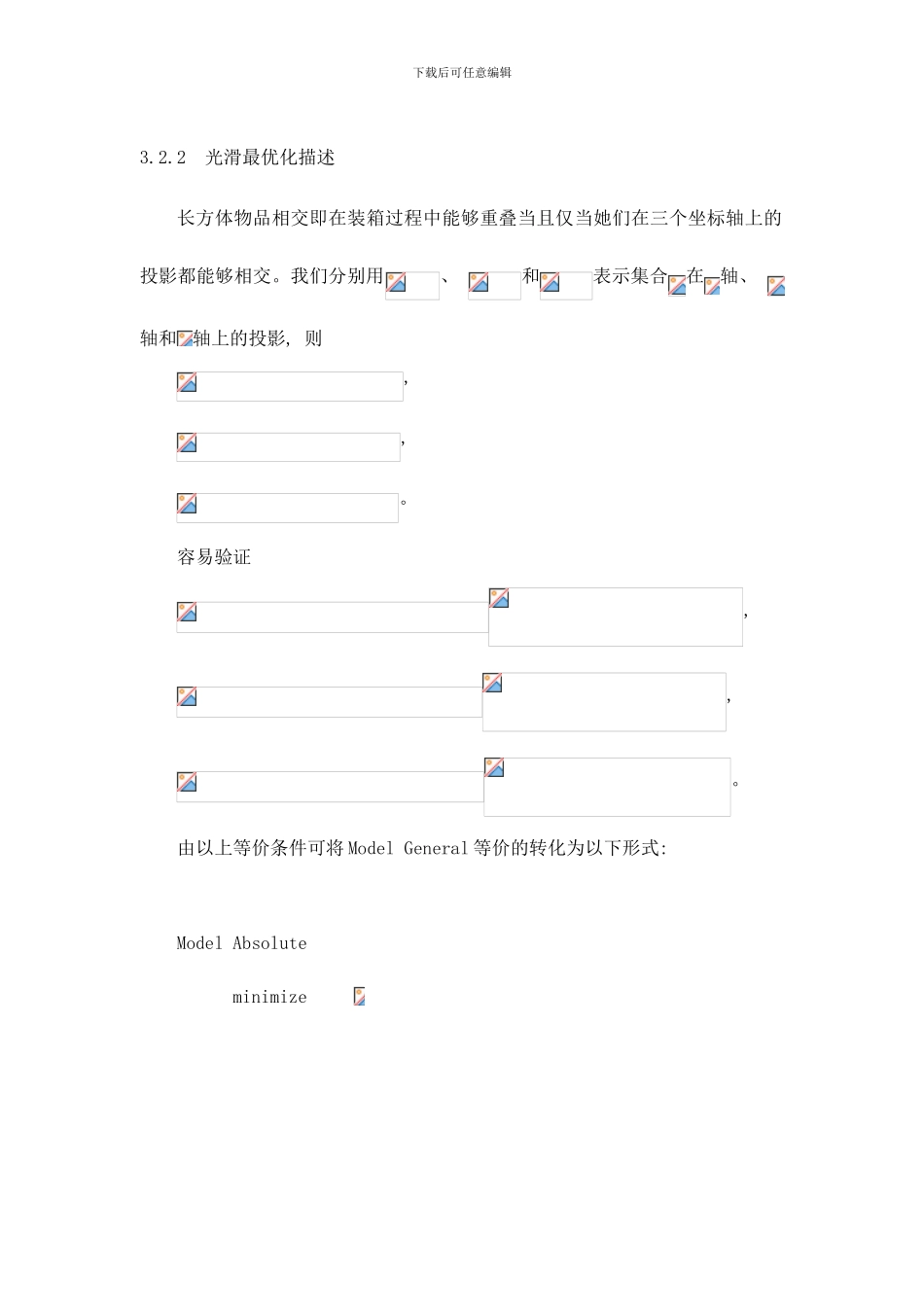
下载后可任意编辑长方体装箱问题的非线性规划模型现有一批立方体形状货物, 要求装入一个集装箱中, 装箱达到的要求为满足一定约束条件下体积的利用率最大化。为便于讨论作如下假定: 货物的几何中心即为其重心, 货物的摆放必须与坐标轴平行( 即在装箱过程中, 要求立方体形状货物的宽、 高、 深均分别与集装箱的宽、 高、 深平行) , 不能斜放, 也不能悬浮放置。装载约束条件为货物理论上能够放在容器的任意位置, 但不能超出容器的容纳范围, 也不能与其它货物交叠放置。1 一般数学模型给定个长方体物品的集合, 每一个成方体物品的宽度、 高度、 深度分别是、 、 , 。给定一个大的长方体箱子, 它的宽度是, 深度是, 高度无限, 要求将这个长方体的小物品装入箱子中, 使小长方体物品的宽度方向、 高度方向、 深度方向分别与大的长方体箱子的宽度方向、 高度方向、 深度方向分别平行, 并使得所用的大长方体箱子的高度最小。采纳的坐标系为三维笛卡尔坐标系, 设坐标系以容器的宽度方向为轴, 高度方向为轴, 深度方向为轴, 容器的左后下角为坐标原点。令是决策变量, 它的第 个重量表示第 个小的长方体物品的左后下角的坐标。定义集合的映射图如下: 下载后可任意编辑其中的定义域是。令, 则中元素的个数为。任意两个长方体的物品装箱时不重叠的充分必要条件是显然, 三维带形装箱问题能转化成以下的优化模型: Model General minimize subject to , , 这 个 数 学 模 型 是 一 个 非 光 滑 模 型 , 因 为 它 的 约 束 条 件是非正常函数。下载后可任意编辑3.2.2 光滑最优化描述长方体物品相交即在装箱过程中能够重叠当且仅当她们在三个坐标轴上的投影都能够相交。我们分别用、 和表示集合在轴、 轴和轴上的投影, 则, , 。容易验证, , 。由以上等价条件可将 Model General 等价的转化为以下形式: Model Absoluteminimize 下载后可任意编辑 subject to Model Absolute 是一非凸非光滑优化模型, 因为其可行集是非凸的。由于, 我们能够经过引进新的变量把 Model Absolute 转化为一个光滑的优化模型。引进变量, 令, , 定义函数, 如下所示: , , 其中, , 下载后可任意编辑, 。令, 其中, , 其中。则 Model Absolute 能转化为以下的光滑优化模型: Model NLPminimize subject to 为了得到 Model NLP 的一阶最优性条件我们引进以下记号下载后可任...