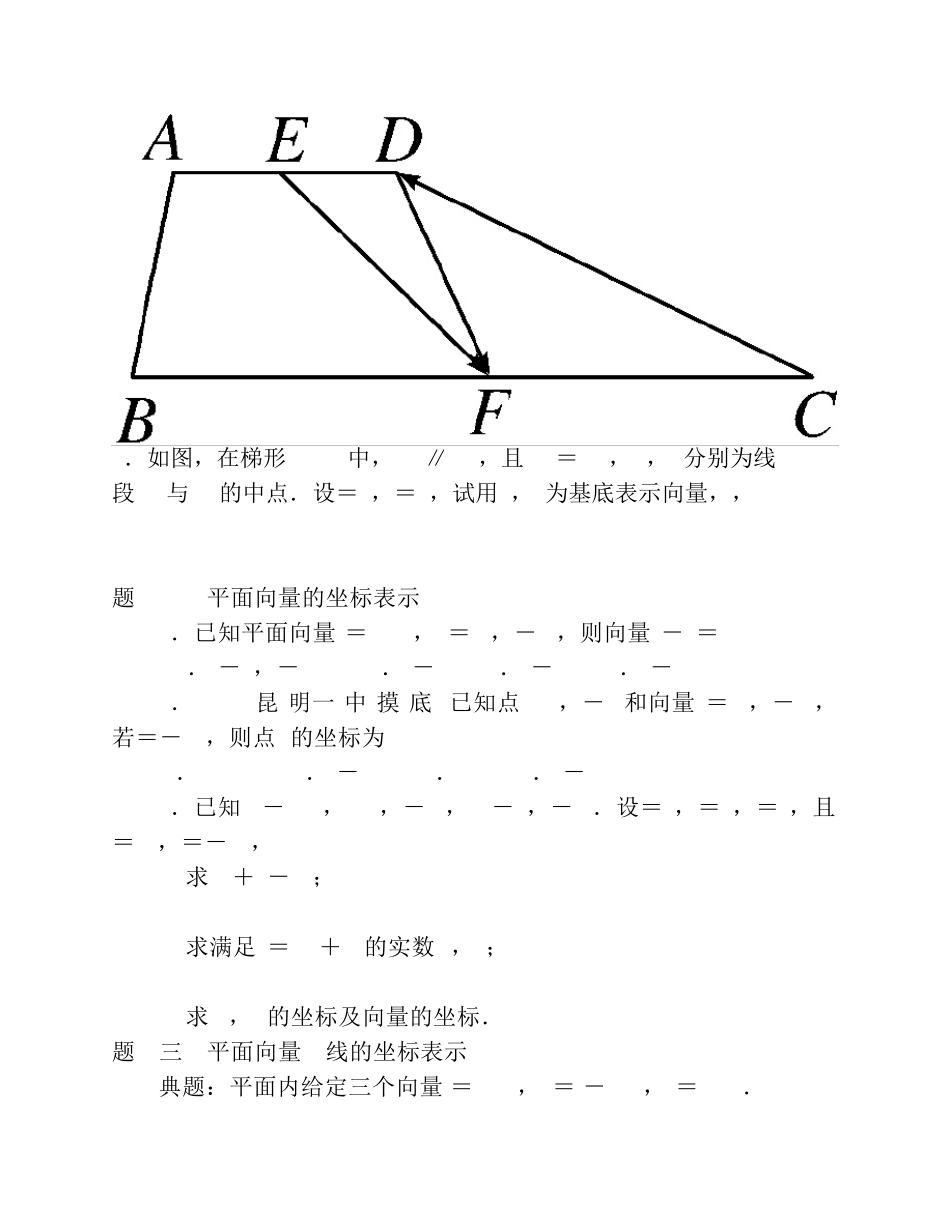
平面向量专题复习考点一、平面向量的概念,线性表示及共线定理题型一、平面向量的概念1.给出下列命题:①若|a|=|b|,则a=b;②若A,B,C,D是不共线的四点,则=是四边形ABCD为平行四边形的充要条件;③若a=b,b=c,则a=c;④a=b的充要条件是|a|=|b|且a∥b;⑤若a∥b,b∥c,则a∥c.其中正确命题的序号是( ) A.②③ B.①② C.③④ D.④⑤2.设a0为单位向量,下列命题中:①若a为平面内的某个向量,则a=|a|·a0;②若a与a0平行,则a=|a|a0;③若a与a0平行且|a|=1,则a=a0.假命题的个数是( ) A.0 B.1 C.2 D.3 题型二、平面向量的线性表示1.(2014·新 课 标 全 国 卷Ⅰ)设D,E,F分别为△ABC的三边BC,CA,AB的中点,则+=( )A. B. C. D.2.(2013·江 苏 高 考)设D,E分别是△ABC的边AB,BC上的点,AD=AB,BE=BC.若=λ1+λ2 (λ1,λ2为实数),则λ1+λ2的值为________.3.(2015·聊 城 二 模 )在△ABC中,=c,=b.若点D满足=2,则=( )A.b+c B.c-b C.b-c D.b+c4.若典例2条件变为:若=2,=+λ,则λ=________. 题型三、平面向量共线定理典题:设两个非零向量e1和e2不共线.如果=e1+e2,=2e1-3e2,=3e1-ke2,且A,C,F三点共线,求k的值. [变式1] 在本例条件下,试确定实数k,使ke1+e2与e1+ke2共线. 考点二、平面向量基本定理及其坐标表示题型一、平面向量基本定理及其应用1.如果e1,e2是平面α内一组不共线的向量,那么下列四组向量中,不能作为平面内所有向量的一组基底的是( ) A.e1与e1+e2 B.e1-2e2与e1+2e2 C.e1+e2与e1-e2 D.e1+3e2与6e2+2e12.如图,在梯形ABCD中,AD∥BC,且AD=BC,E,F分别为线段AD与BC的中点.设=a,=b,试用a,b为基底表示向量,,. 题型二、平面向量的坐标表示1.已知平面向量a=(1,1),b=(1,-1),则向量a-b=( )A.(-2,-1) B.(-2,1) C.(-1,0) D.(-1,2)2.(2015·昆 明一 中 摸 底 )已知点M(5,-6)和向量a=(1,-2),若=-3a,则点N的坐标为( )A.(2,0) B.(-3,6) C.(6,2) D.(-2,0)3.已知A(-2,4),B(3,-1),C(-3,-4).设=a,=b,=c,且=3c,=-2b,(1)求3a+b-3c; (2)求满足a=mb+nc的实数m,n; (3)求M,N的坐标及向量的坐标.题型三、平面向量共线的坐标表示典题:平面内给定三个向量a=(3,2),b=(-1,2),c=(4,1).(1)求满足a=mb+nc的实数m,n; ...