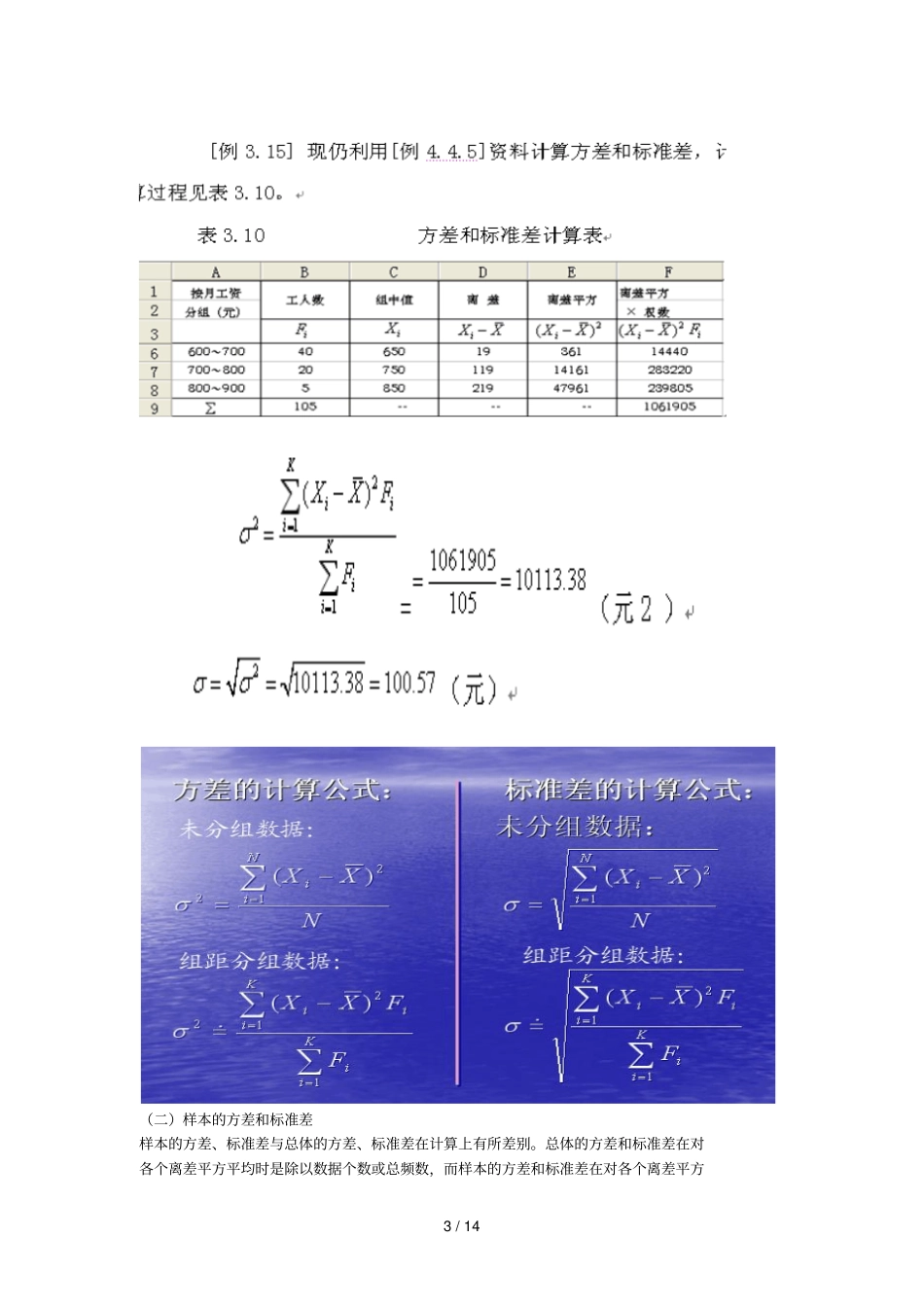
1 / 14 第五章离散趋势测量法第二节、全距与四分位差?一、全距?1、未分组资料计算公式?全距又称极差,是一组数据的最大值与最小值之差,用表示。计算公式为:??式中,、分别表示为一组数据的最大值与最小值。由于全距是根据一组数据的两个极值表示的,所以全距表明了一组数据数值的变动范围。越大,表明数值变动的范围越大,即数列中各变量值差异大,反之,越小,表明数值变动的范围越小,即数列中各变量值差异小。2、分组资料计算公式R= 最高组上限- 最低组下限?R= 最高组组中组 -最低组组中值?R= 最高组组中组 -最低组下限?R= 最高组上限 -最低组组中值?如果资料经过整理,并形成组距分配数列,全距可近似表示为:?R≈最高组上限值-最低组下限值3、优缺点:优点:计算简单,易于理解。缺点:(1)受极端值影响大,遇含开口组的资料时无法计算;(2)数据利用率低,信息丧失严重;(3)受抽样变动影响大(一般大样本的全距会比小样本的全距大)。二、四分位差(inter-quartile range )上四分位数与下四分位数之差的平均数,称为四分位差,亦称为内距或四分间距。四分位差的计算方法:Q· D=(Q3-Q1) /2 四分位差反映了中间50% 数据的离散程度,其数值越小,说明中间的数据越集中;数值越大,说明中间的数据越分散。此外,由于中位数处于数据的中间位置,因此,四分位差的大小在一定程度上也说明了中位数对一组数据的代表程度。四分位差主要用于测度顺序数据的离散程度。当然,对于数值型数据也可以计算四分位差,但不适合于分类数据。优缺点:主要是避免了全距受极端值影响的缺点,其他优缺点同全距:数据利用率低,信息丧失严重;受抽样变动影响大。max()min()iiRXXmax( )iXmin()iX2 / 14 第三节、平均差?平均差是各变量值与其算术平均数离差绝对值的平均数,用A.D 表示。根据掌握资料的不同,平均差有以下两种计算方法:?1. 简单平均法?对于未分组资料,采用简单平均法。其计算公式为:2. 加权平均法在资料分组的情况下,应采用加权平均式第四节、方差和标准差?一、概念要点?方差和标准差同平均差一样,也是根据全部数据计算的,反映每个数据与其算术平均数相比平均相差的数值,因此它能准确地反映出数据的差异程度。但与平均差不同之处是在计算时的处理方法不同,平均差是取离差的绝对值消除正负号,而方差、标准差是取离差的平方消除正负号,这更便于数学上的处理。因此,方差、标准差是实际中应用最广泛的离中程度...