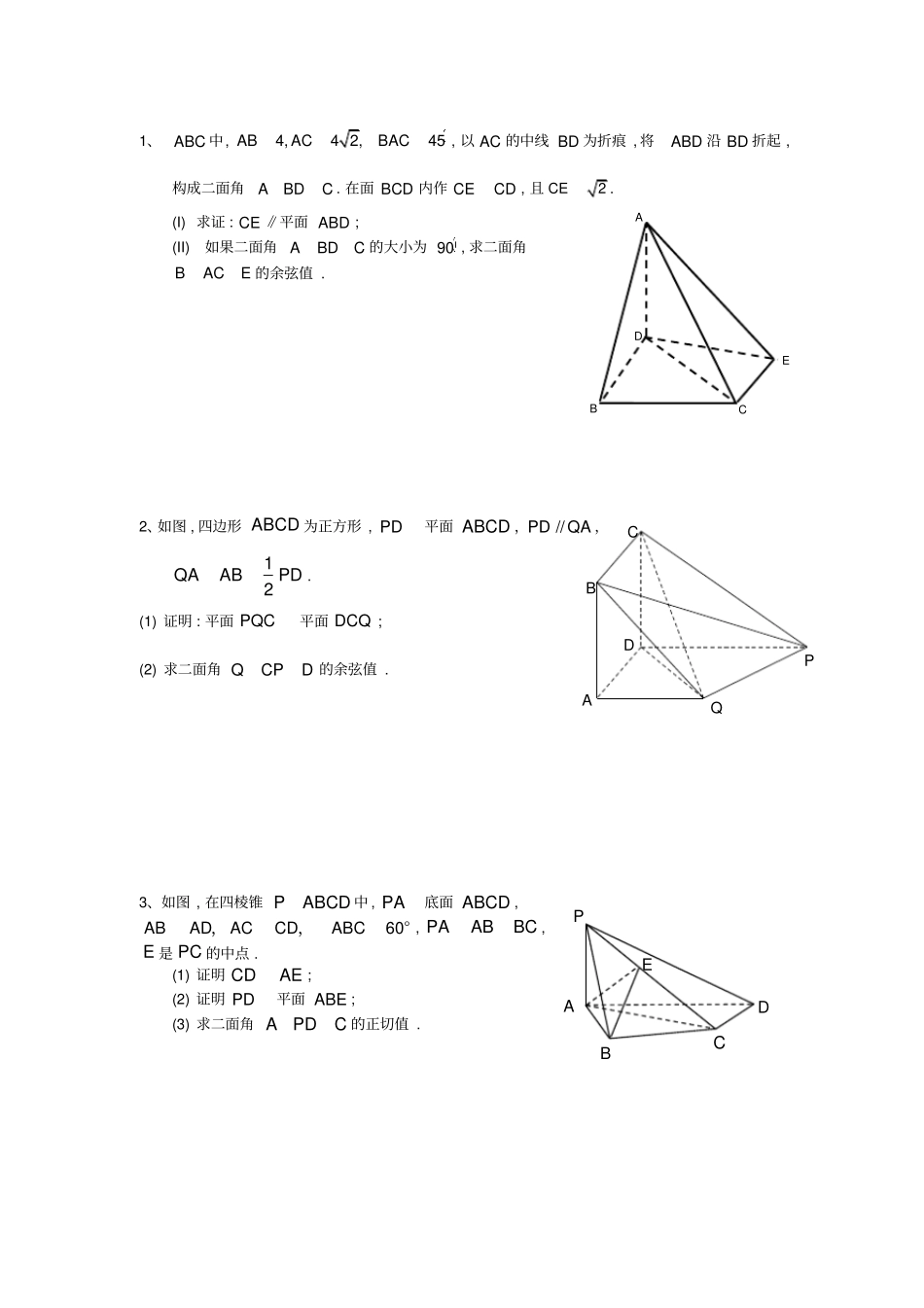
ABCDEABCDPEQPDCBA1、ABC 中,4,4 2,45ABACBAC, 以 AC 的中线 BD 为折痕 , 将ABD 沿 BD 折起 ,构成二面角ABDC . 在面 BCD 内作 CECD , 且2CE. (I) 求证 : CE ∥平面 ABD ; (II)如果二面角ABDC 的大小为 90 , 求二面角BACE 的余弦值 . 2、如图 , 四边形 ABCD 为正方形 , PD平面 ABCD ,QAPD //,PDABQA21. (1) 证明 : 平面 PQC平面 DCQ ; (2) 求二面角 QCPD 的余弦值 . 3、如图 , 在四棱锥 PABCD 中 , PA底面 ABCD , 60ABADACCDABC,,° , PAABBC , E 是 PC 的中点 . (1) 证明 CDAE ; (2) 证明 PD平面 ABE ; (3) 求二面角 APDC 的正切值 . 4、如图 , 三棱锥 P-ABC中, ∠ACB=90° ,PA⊥底面 ABC. (I) 求证 : 平面 PAC⊥平面 PBC; (II)若 AC=BC=PA,M是 PB的中点 , 求 AM与平面 PBC所成角的正切值. 5、已知四棱锥ABCDP, PA底面 ABCD ,ACADABBCAD,,//与 BD 交于点O , 又,6,32,2,3BCABADPA( Ⅰ ) 求 证 :BD平 面 PAC ;(Ⅱ ) 求 二 面 角APBO的 余弦 值 . 参考答案1、【答案】解:(1) 由4,4 2,45ABACBAC得4BC, 所以ABC 为等腰直角三角形 , 由 D 为 AC 的中点得BDAC , 以 AC 的中线BD 为折痕翻折后仍有BDCD , 因为 CECD , 所以CE ∥ BD , 又 CE平面 ABD , BD平面 ABD , 所以CE ∥平面 ABD . (2) 如果二面角ABDC 的大小为90 , 由 ADBD得 AD平面 BDC , 因此 ADCE , 又 CECD , 所以CE平 面ACD,从而CEAC.由 题 意ABCDEFG2 2ADDC, 所以 Rt ADC 中,4AC. 设 BC 中点为 F , 因为4ABBC, 所以BFAC , 且23BF, 设 AE 中点为 G , 则 FG ∥ CE , 由 CEAC 得 FGAC , 所以BFG为 二 面 角BACE的 平 面 角 ,连 结BG ,在BCE 中 , 因 为4,2,135BCCEBCE,所以26BE.在Rt DCE中22(22)( 2)10DE, 于 是 在 Rt ADE 中 ,22(22)( 10)3 2AE. 在ABE中,2222111332242BGABBEAE,所以在BFG中,13312622cos322 2 32BFG. 因此二面角BACE 的余弦值为63. 2、【答案】 (1),,,,,PDABCD PDCDCDDAQPCDPQPQDQPQCDQ PQPCQ面又CDAD面又面面面PQC面DCQ.(2) 过 Q 作 QOPQ 交于点O,过 O 作 OM PC 交于点M.则OMQ 是二面角 的平面角.6cos6OMQ3、【答案】 解答 :( Ⅰ) 证明 : 在四棱锥 PABCD 中, 因 PA底面 ABCD , CD平...