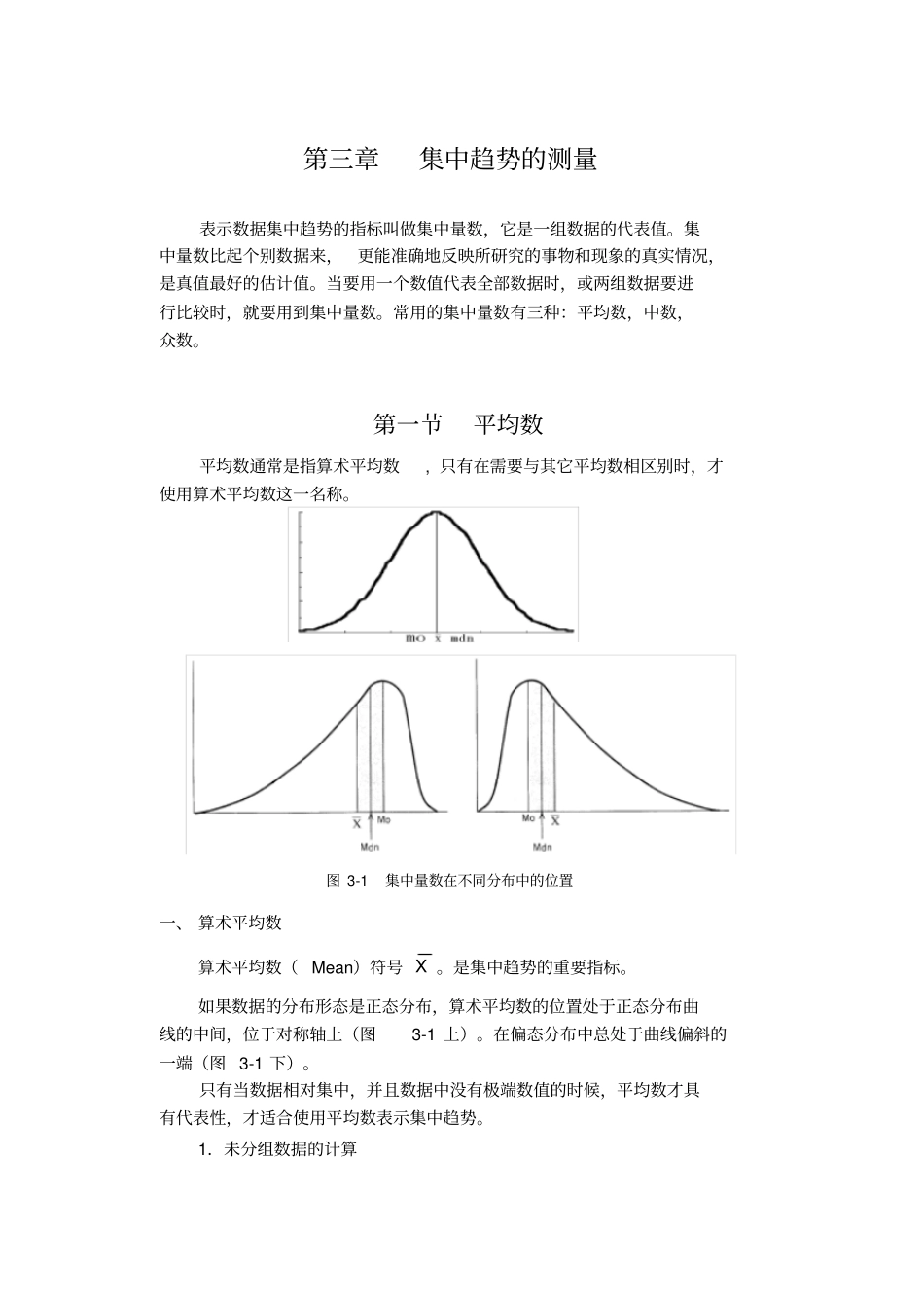
第三章集中趋势的测量表示数据集中趋势的指标叫做集中量数,它是一组数据的代表值。集中量数比起个别数据来,更能准确地反映所研究的事物和现象的真实情况,是真值最好的估计值。当要用一个数值代表全部数据时,或两组数据要进行比较时,就要用到集中量数。常用的集中量数有三种:平均数,中数,众数。第一节平均数平均数通常是指算术平均数, 只有在需要与其它平均数相区别时,才使用算术平均数这一名称。图 3-1 集中量数在不同分布中的位置一、 算术平均数算术平均数( Mean)符号 X 。是集中趋势的重要指标。如果数据的分布形态是正态分布,算术平均数的位置处于正态分布曲线的中间,位于对称轴上(图3-1 上)。在偏态分布中总处于曲线偏斜的一端(图 3-1 下)。只有当数据相对集中,并且数据中没有极端数值的时候,平均数才具有代表性,才适合使用平均数表示集中趋势。1.未分组数据的计算计算未分组数据的平均数,是用全部数据的和除以数据个数。所得的值为整组数据的代表。数据少时使用计算器较为方便。平均数的计算公式:NXX(3.1)式中, X :原始数据;Σ :求和符号(希腊字母,读:sigma),表示将所有的数据都加起来;N:数据个数;2.分组数据的计算当数据较多,或需要了解数据的分布形态已将数据分组后,可利用已列好的次数分布表计算平均数。NXfX(3.2)式中, f:各小组的数据个数;X’:各小组中数;Σ :和号;N:数据总个数。例题 3-2:一项心理测验成绩得出的次数分布表如下,请求出平均成绩。表 3-1 心理测验成绩分数X ’F FX ’35-39 37 5 185 30-34 32 12 384 25-29 27 20 540 20-24 22 27 594 15-19 17 25 425 10-14 12 19 228 5 – 9 7 7 49 Σ/ 115 2405 计算步骤:(1)在表中求出各组次数与各组中点的乘积列fX’列。(2)累加各组次数f 列、得出总数115 (3)累加乘积fX’列、得出总数2405。(4)用公式 3.2 求出X 。计算:9.201152405NXfX答: 115 人的成绩平均数为20.9 分。二、 加权平均数加权平均数符号WX 。由于数据n 不等时各小组平均数所代表的数据个数不等。此时各小组平均数的意义对于总平均数就不同,因此在计算总平均数时要考虑小组n 的权重,而采用加权的方法。1.加权平均数的计算计算公式:nXnX W)((3.3) 式中WX :加权平均数;Σ :和号;n:小组数据个数。2.加权百分数的计算计算公式nnpXPW)((3.4)式中PWX:加权百分数;Σ...