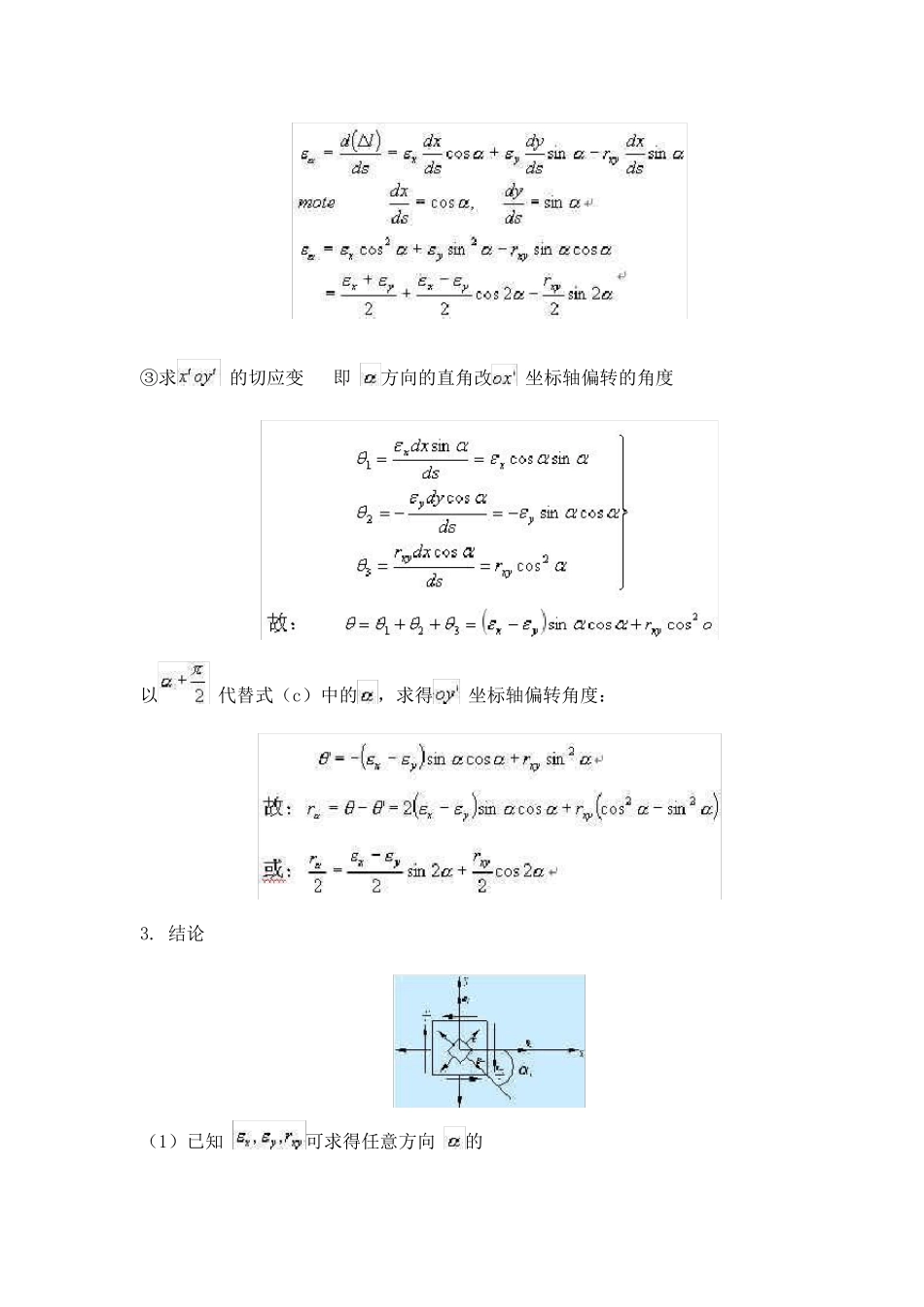
1. 概述 (1)平面应变状态:即受力构件表面一点处的应变情况。 (2)测试原理: 一般最大应变往往发生在受力构件的表面。通常用应变仪测出受力构件表面一点处三个方向的线应变值,然后确定该点处的最大线应变和最小应变及其方程。 2. 公式推导: (1)选定坐标系为xoy,如图示 (2)设0 点处, 为已知。 规定伸长为正,切应变 以xoy 直角增大为正。 (3)求任意方向, 方向( 规定逆时针方向为正)的线应变 和切应变 (即 直角的改变量)。 (4)叠加法:求 方向的线应变 和切应变 ①由于 而引起 ds 的长度改变 , ② 方向(即 方向)的线应变 ③求 的切应变 即 方向的直角改 坐标轴偏转的角度 以 代替式(c)中的,求得 坐标轴偏转角度: 3. 结论 (1)已知 可求得任意方向 的 (2)已知 ,求得 (3)主应变和主应变方向 比较上述公式,可见 故: 4. 应变圆 5. 应变的实际测量 ①用解析法或图解法求一点处的主应变时,首先必须已知 ,然而用应变仪直接测量时, 可以测试,但 不易测量。所以,一般是先测出任选三个方向 的线应变 。 ②然后利用一般公式,将 代入 得出: 联解三式,求出,于是再求出主应变的方向与数值 ④由③ 式求出 ,当 时 与二、四相限的角度相对应。 6. 直角应变花(45°应变花)测量 为了简化计算,三个应变选定三个特殊方向 测得: ,代入 一般公式 求得: 故 讨论: 若 与二、四相限的角度相对应。见 P257、7.21 题 6. 等角应变花测量 一般公式: 测定值: 代入式(a)得: 主应变方向: 故: 于是由主应变公式: ,穿过二,四相限.见P258,7.22 题 Example 1. 用直角应变花测得一点的三个方向的线应变 Find:主应变及其方向 Solution: 故 过二、四相限。 Example2. 若已测得等角应变花三个方向的线 试求主应变及其方向 Solution: 即: 应力测量 (measurement of stress) 测量物体由于外因或内在缺陷而变形时,在它内部任一单位截面积上内外两方的相互作用力。应力是不能直接测量的,只能是先测出应变,然后按应力与应变的关系式计算出应力。若主应力方向已知,只要沿着主应力方向测出主应变,就可算出主应力。各种受力情况下的应变值的测量方法见表1。 轴向拉伸(或压缩)时,沿轴向力方向粘贴应变片(表l 之1~4),测出应变ε,按单向虎克定律算出测点的拉(压)应力σ=εE。式中ε 为应变,E 为弹性模量。 弯曲...