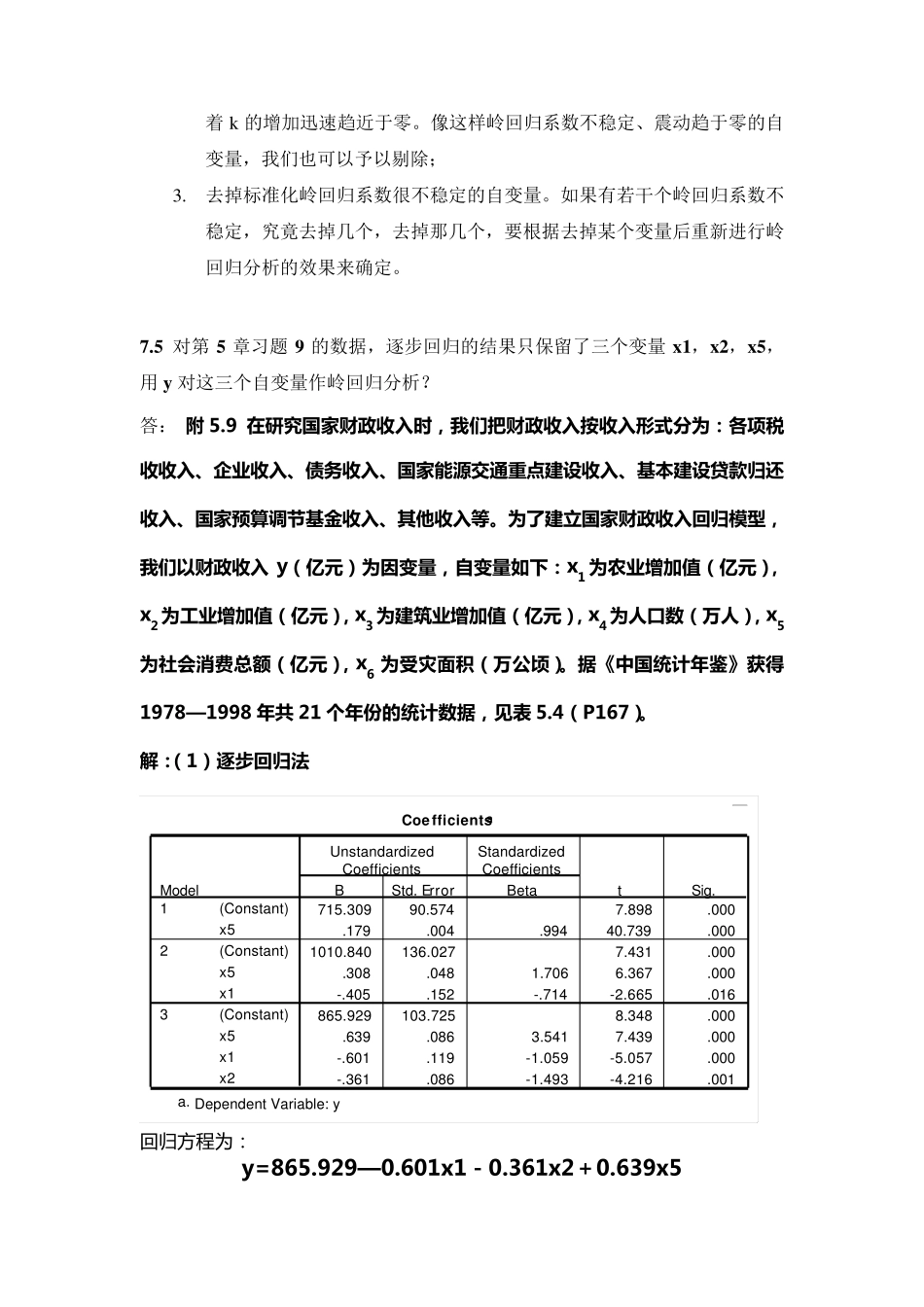
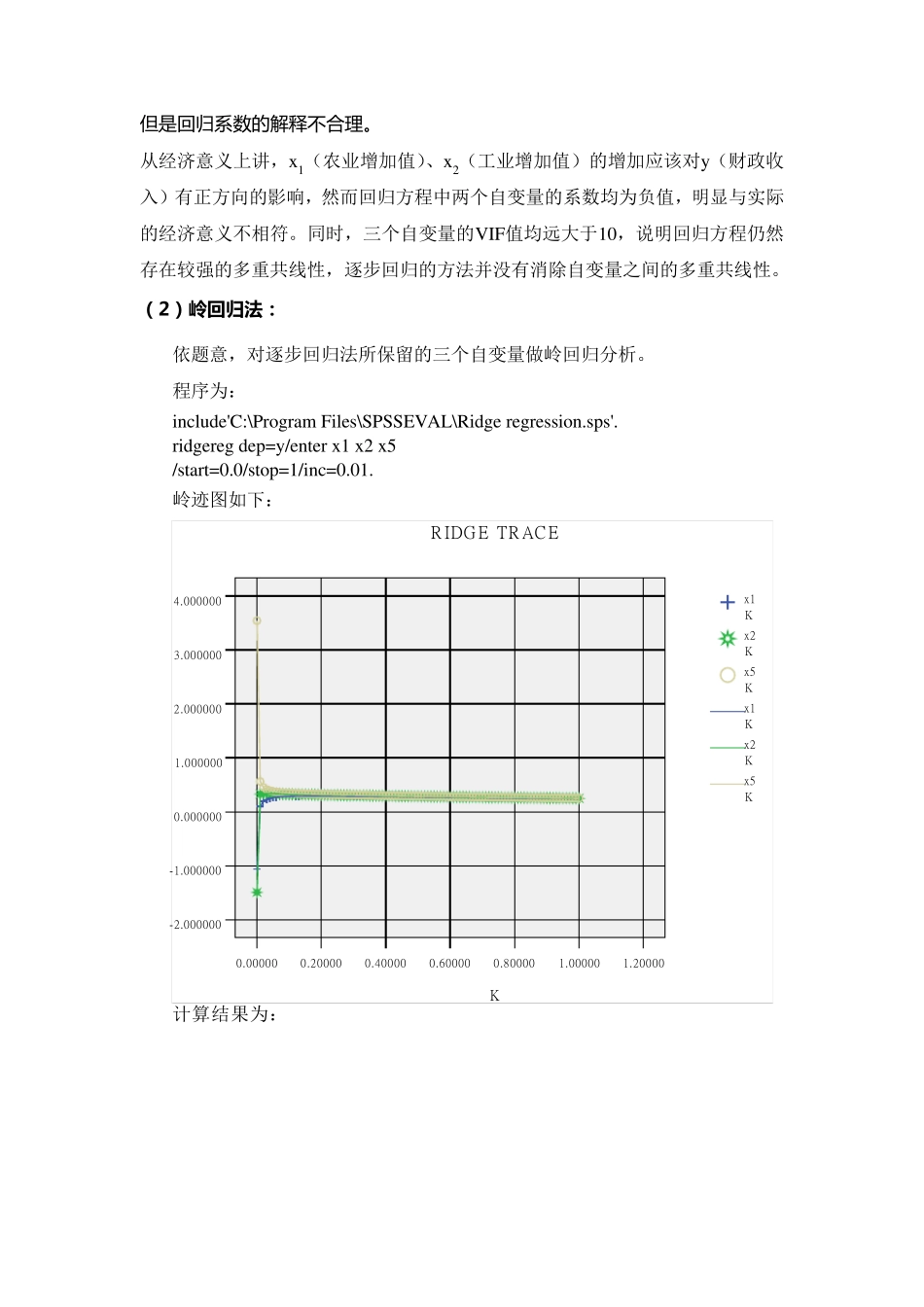
第7 章 岭回归 思考与练习参考答案 7.1 岭回归估计是在什么情况下提出的? 答:当自变量间存在复共线性时,|X’X|≈0,回归系数估计的方差就很大, 估计值就很不稳定,为解决多重共线性,并使回归得到合理的结果,70 年代提出了岭回归(Ridge Regression,简记为RR)。 7.2 岭回归的定义及统计思想是什么? 答:岭回归法就是以引入偏误为代价减小参数估计量的方差的一种回归方法,其统计思想是对于(X’X)-1为奇异时,给 X’X 加上一个正常数矩阵 D, 那么X’X+D接近奇异的程度就会比 X′X 接近奇异的程度小得多,从而完成回归。但是这样的回归必定丢失了信息,不满足 blue。但这样的代价有时是值得的,因为这样可以获得与专业知识相一致的结果。 7.3 选择岭参数k 有哪几种方法? 答:最优k 是依赖于未知参数 和2 的,几种常见的选择方法是: ○1 岭迹法:选择0k 的点能使各岭估计基本稳定,岭估计符号合理,回归系数没有不合乎经济意义的绝对值,且残差平方和增大不太多; ○2 方差扩大因子法:11( )()()c kX Xk IX X X Xk I,其对角线元( )jjck 是岭估计的方差扩大因子。要让( )10jjck; ○3 残差平方和:满足( )SSE kcSSE成立的最大的k 值。 7.4 用岭回归方法选择自变量应遵循哪些基本原则? 答:岭回归选择变量通常的原则是: 1. 在岭回归的计算中,我们通常假定涉及矩阵已经中心化和标准化了,这样可以直接比较标准化岭回归系数的大小。我们可以剔除掉标准化岭回归系数比较稳定且绝对值很小的自变量; 2. 当k 值较小时,标准化岭回归系数的绝对值并不很小,但是不稳定,随着k 的增加迅速趋近于零。像这样岭回归系数不稳定、震动趋于零的自变量,我们也可以予以剔除; 3 . 去掉标准化岭回归系数很不稳定的自变量。如果有若干个岭回归系数不稳定,究竟去掉几个,去掉那几个,要根据去掉某个变量后重新进行岭回归分析的效果来确定。 7 .5 对第 5 章习题 9 的数据,逐步回归的结果只保留了三个变量 x 1 ,x 2 ,x 5 ,用 y 对这三个自变量作岭回归分析? 答: 附 5.9 在 研 究 国 家 财 政 收 入 时 , 我 们 把 财 政 收 入 按 收 入 形 式 分 为 : 各 项 税收 收 入 、企 业 收 入 、债 务 收 入 、国 家 能 源 交 通 重 点 建 设 收 入 、基 本 建 设 贷 款 归 还收 入...