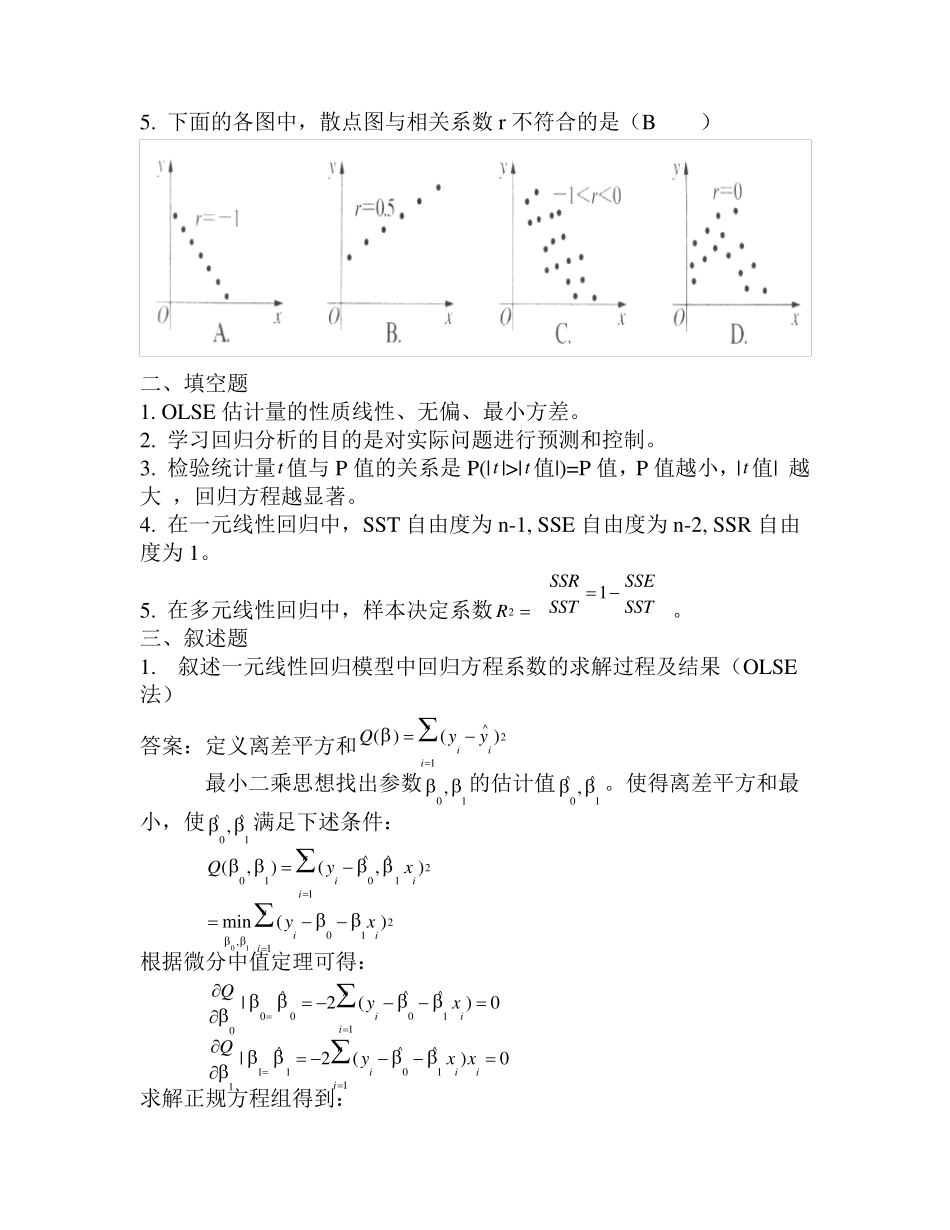
应用回归分析试题(一) 一、选择题 1. 两个变量与x的回归模型中,通常用2R 来刻画回归的效果,则正确的叙述是( D ) A. 2R 越小,残差平方和越小 B. 2R 越大,残差平方和越大 C. 2R 与残差平方和无关 D. 2R 越小,残差平方和越大 2.下面给出了4 个残差图,哪个图形表示误差序列是自相关的(B) (A) (B) (C) (D) 3.在对两个变量x,y进行线性回归分析时,有下列步骤: ①对所求出的回归直线方程作出解释; ②收集数据(ix ,iy ),1,2i ,…,n;③求线性回归方程; ④求未知参数; ⑤根据所搜集的数据绘制散点图 如果根据可行性要求能够作出变量,x y具有线性相关结论,则在下列操作中正确的是( D ) A.①②⑤③④ B.③②④⑤① C.②④③①⑤ D.②⑤④③① 4.下列说法中正确的是(B ) A.任何两个变量都具有相关关系 B.人的知识与其年龄具有相关关系 C.散点图中的各点是分散的没有规律 D.根据散点图求得的回归直线方程都是有意义的 12345678xe0y5. 下面的各图中,散点图与相关系数r 不符合的是(B ) 二、填空题 1. OLSE 估计量的性质线性、无偏、最小方差。 2. 学习回归分析的目的是对实际问题进行预测和控制。 3. 检验统计量t值与P 值的关系是P(|t|>|t值|)=P 值,P 值越小,|t 值| 越大 ,回归方程越显著。 4. 在一元线性回归中,SST 自由度为 n-1, SSE 自由度为 n-2, SSR 自由度为 1。 5. 在多元线性回归中,样本决定系数2R 1SSRSSESSTSST 。 三、叙述题 1. 叙述一元线性回归模型中回归方程系数的求解过程及结果(OLSE法) 答案:定义离差平方和2^1)()(iniiyyQ 最小二乘思想找出参数10,的估计值^1^0,。使得离差平方和最小,使^1^0,满足下述条件: niiiniiixyxyQ1210,121^^010)(min),(),(10 根据微分中值定理可得: 0)(2|0)(2|^11^01^11^11^00^00iiniiiniixxyQxyQ 求解正规方程组得到: niiniiixxyyxxxy121^11^^0)())(( 令 yxnyxyyxxLxnxxxLniiiiniixyniiniixx1121212)()()( 则一元线性回归模型中回归方程系数可表示为 2. 叙述多元线性回归模型的基本假设 答案:假设1.解释变量12,,,KXXX ...