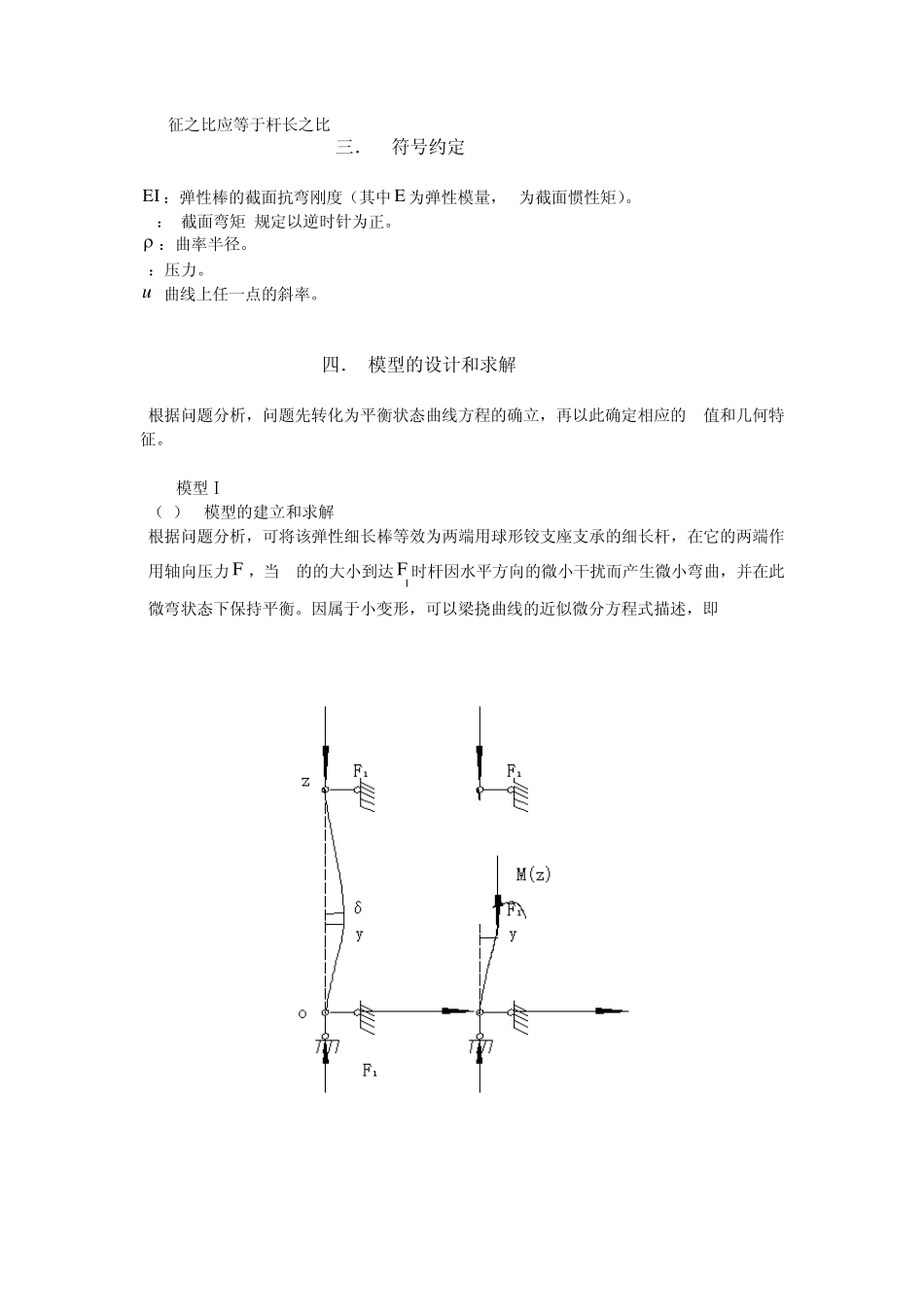
弹性棒的弯曲变形研究 案例背景 对于某一均匀圆柱形细长弹性棒,在棒的两端施加方向相反大小相等(等于 F )的轴向压力. 实验表明,当且仅当 F 大于某力 F1 时,棒才会发生弯曲. 这个 力 F1 称为临界力. 而当 F = F2 ≈ 2F1 时,棒的平衡状态如示意图 1 那样:棒的两 个端点重合(假设棒仍处在弹性限度之内). 试建立数学模型来验证实验的结果.并且完成以下任务: 一、计算力学特征: 1. 临界力 F1 的表达式; 2. F2 / F1 的精确的理论比值. 二、计算 F = F2 时棒的平衡状态曲线的几何特征: 1.宽度与棒长之比; 2.高度与棒长之比; 3.端点重合处的夹角(单位:度). 示意图 1 一.问题的分析 仔细思考问题的条件和要求,思考如下: 1. 工作前奏——概念理解 F2 / F1 的精确的理论比值,通过对材料力学和数学的理解,并查阅了相关资料,认为它是指相对于给定的,这里的精确不是指误差为 0,而是指在允许的范围内较 2更为精确的比值,比值越精确,模型越是合理。 2. 中心任务——建立在2F 作用下弹性棒的的曲线方程并求解 (1) 问题转化。问题要求确定一个精确21/FF 比值,以及计算出 F = F2 时棒的平衡状态曲线的几何特征;即使要求建立一个合理的曲线方程模型来表示弹性棒的变形,并通过解此方程球的相应的几何特征。 (2) 具体方法。具体方法是否得当,不仅仅是该模型建立本身的合理性、逻辑严密性,而且要求该模型具有可解性,即该模型能够通过现有的数学手段求解。 从 F1的求解入手,层层递进,使模型逐步优化。 1) 按照纯弯曲理论,对细长杆小变形压杆失稳用梁挠曲线近似微分方程式按照材料力学公式求解——即欧拉公式。 2) 在 1)的基础上,对大变形理想弹性棒进行分析,据结构力学对称性分析,将 F2作用下的弹性棒简化为一端固定,一端自由的弹性棒,类比欧拉公式,得出其挠曲线微分方程。 3) 对该方程进行进一步分析和简化,发现其是不可积方程,故对该方程利用进行优化,通过在固定端的近似求解,将弹性棒的变形曲线分解成两段。通过边界条件,近似解出该方程。 3. 目标工作 得到该方程后,代入相应条件,得出曲线的几何特征。 4. 模型反思 在支座附近曲线求解上采取了近似处理,将整个棒上弯矩取为常数自由端弯矩,事实上,并非常数。截断点离固端越近,求解越是精确。 二. 模型假设 1. 棒是均匀的,圆柱形的,细长弹性的。 2. 棒的截...