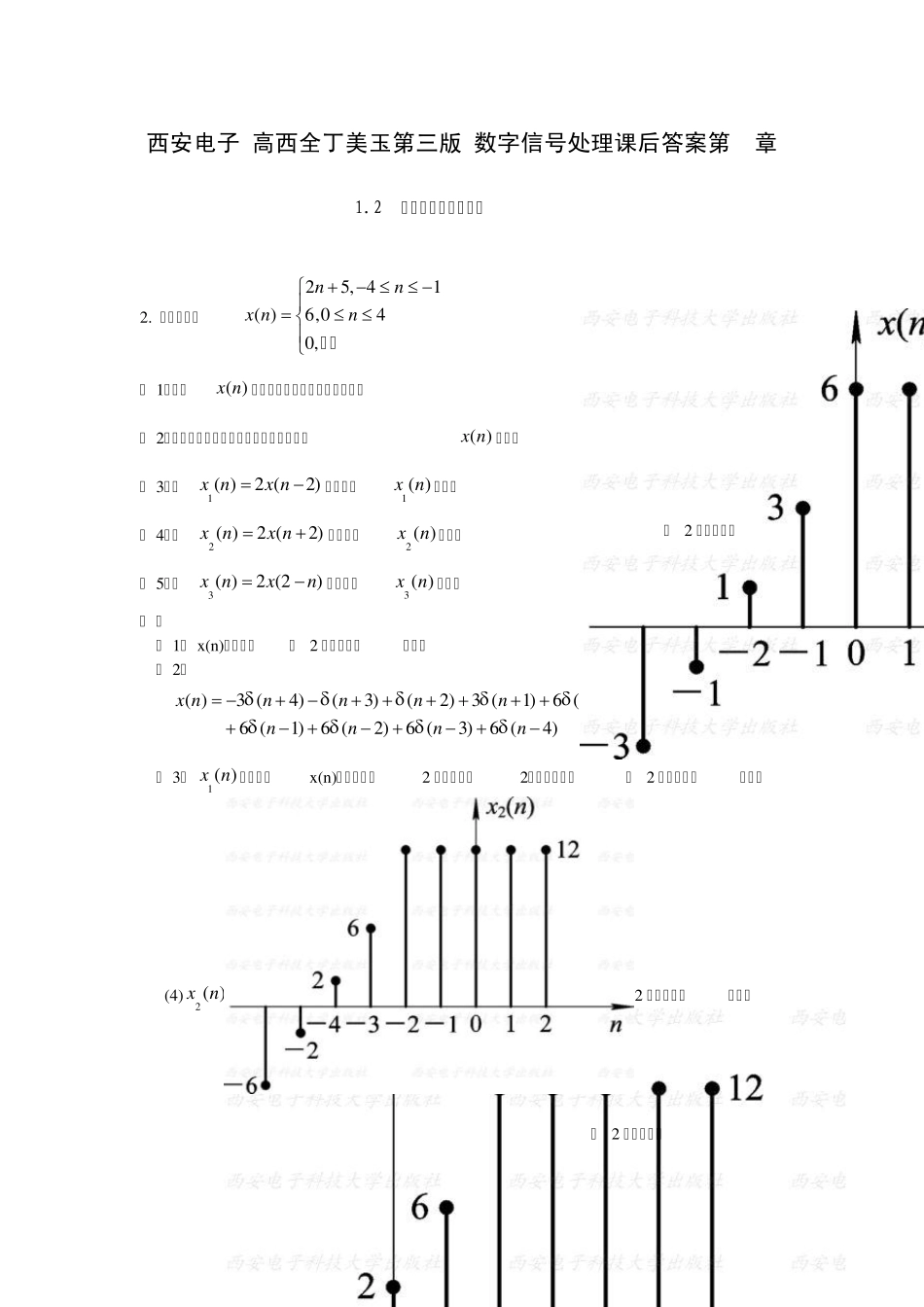
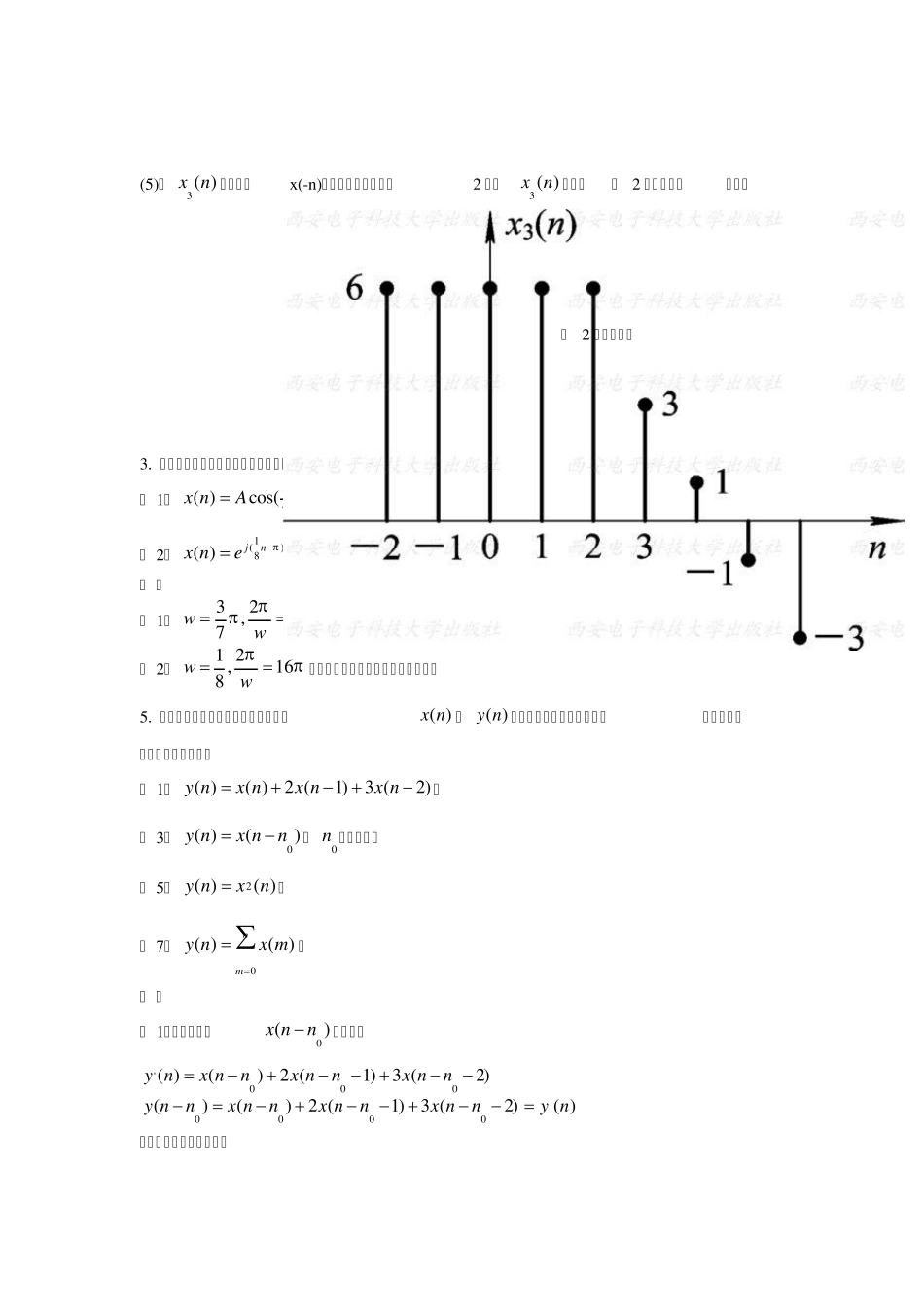
西安电子(高西全丁美玉第三版)数字信号处理课后答案第 2章 1.2 教材第一章习题解答 2 . 给定信号:25 , 41( )6 ,040 ,nnx nn 其它 ( 1 )画出( )x n 序列的波形,标上各序列的值; ( 2 )试用延迟单位脉冲序列及其加权和表示( )x n 序列; ( 3 )令1 ( )2 (2 )x nx n,试画出1 ( )x n 波形; ( 4 )令2 ( )2 (2 )x nx n,试画出2 ( )x n 波形; ( 5 )令3 ( )2 (2)x nxn,试画出3 ( )x n 波形。 解 : ( 1 ) x (n )的波形如题 2 解图(一)所示。 ( 2 ) ( )3(4 )(3 )(2 )3(1 )6( ) 6(1 )6(2 )6(3 )6(4 )x nnnnnnnnnn ( 3 )1 ( )x n 的波形是x (n )的波形右移2 位,在乘以2 ,画出图形如题 2 解图(二)所示。 (4 )2 ( )x n 的波形是x (n )的波形左移2 位,在乘以2 ,画出图形如题 2 解图(三)所示。 题 2 解图(一) 题 2 解图(二) 题 2 解图(三) (5)画3( )x n 时,先画x(-n)的波形,然后再右移2 位,3( )x n 波形如题 2 解图(四)所示。 3. 判断下面的序列是否是周期的,若是周期的,确定其周期。 ( 1)3( )cos()78x nAn, A 是常数; ( 2)1()8( )jnx ne。 解 : ( 1)3214,73ww,这是有理数,因此是周期序列,周期是T=14; ( 2)1 2,168ww,这是无理数,因此是非周期序列。 5. 设系统分别用下面的差分方程描述,( )x n 与( )y n 分别表示系统输入和输出,判断系统是否是线性非时变的。 ( 1)( )( )2 (1)3 (2)y nx nx nx n; ( 3)0( )()y nx nn,0n 为整常数; ( 5)2( )( )y nx n; ( 7)0( )( )nmy nx m 。 解 : ( 1)令:输入为0()x nn,输出为'000'0000( )()2 (1)3 (2)()()2 (1)3 (2)( )y nx nnx nnx nny nnx nnx nnx nny n 故该系统是时不变系统。 题 2 解图(四) 12121212( )[( )( )] ( )( )2((1)(1))3((2)(2))y nT ax nbx nax nbx nax nbx nax nbx n 1111[( )]( )2(1)3(2)T ax nax nax nax n 2222[( )]( )2(1)3(2...