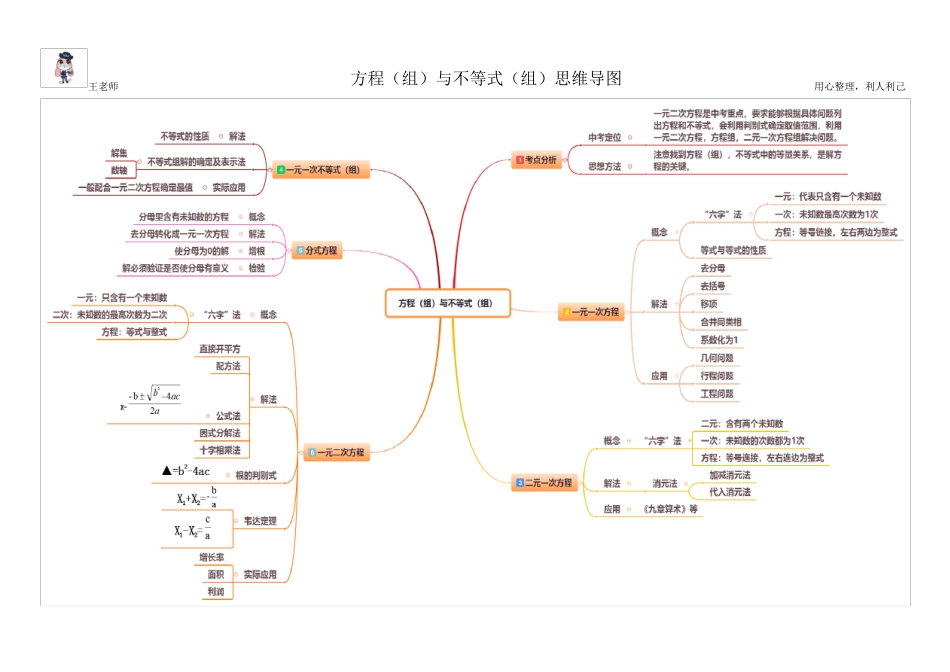
王老师 方程(组)与不等式(组)思维导图 用心整理,利人利己 王老师 方程(组)与不等式(组)思维导图 用心整理,利人利己 一.【考点梳理】 考点一、不等式的相关概念 1.不等式 用不等号连接起来的式子叫做不等式. 常见的不等号有五种: “≠”、 “>” 、 “<” 、 “≥”、 “≤”. 2.不等式的解与解集 不等式的解:使不等式成立的未知数的值,叫做不等式的解. 不等式的解集:一个含有未知数的不等式的解的全体,叫做不等式的解集. 不等式的解集可以在数轴上直观的表示出来,具体表示方法是先确定边界点:解集包含边界点,是实心圆点;不包含边界点,则是空心圆圈;再确定方向:大向右,小向左. 3.解不等式 求不等式的解集的过程或证明不等式无解的过程,叫做解不等式. 要点诠释: 不等式的解与一元一次方程的解是有区别的:不等式的解是不确定的,是一个范围,而一元一次方程的解则是一个具体的数值. 考点二、不等式的性质 性质 1: 不等式两边加上(或减去)同一个数(或式子),不等号的方向不变,即如a>b,那么a±c>b±c. 性质 2: 不等式两边乘以(或除以)同一个正数,不等号的方向不变,即如果a>b,c>0,那么ac>bc(或 ac > bc ). 性质 3: 不等式两边乘以(或除以)同一个负数,不等号的方向改变,即如果a>b,c<0,那么ac<bc(或 ac < bc ). 要点诠释: (1)不等式的其他性质:①若a>b,则 b<a;②若a>b,b>c,则 a>c;③若a≥b,且b≥a,•则 a=b;④ 若a2≤0,则 a=0;⑤ 若ab>0 或王老师 方程(组)与不等式(组)思维导图 用心整理,利人利己 0ab ,则a、b 同号;⑥若ab<0 或0ab ,则a、b 异号. (2)任意两个实数a、b 的大小关系:①a-b>O a>b;②a-b=O a=b;③a-b<O a<b. 不等号具有方向性,其左右两边不能随意交换:但a<b 可转换为b>a,c≥d 可转换为d≤c. 考点三、一元一次不等式(组) 1.一元一次不等式的概念 只含有一个未知数,且未知数的次数是1,系数不等于0 的不等式叫做一元一次不等式.其标准形式:ax+b>0(a≠0)或ax+b≥0(a≠0) ,ax+b<0(a≠0)或ax+b≤0(a≠0). 2.一元一次不等式的解法 一元一次不等式的解法与一元一次方程的解法类似,•但要 特 别 注 意不等式的两边都 乘 以 (或除 以 )同一个负 数时 ,不等号要 改 变 方向. 解一元一次不等式的一般 ...