界面内聚力模型及有限元法VIP免费

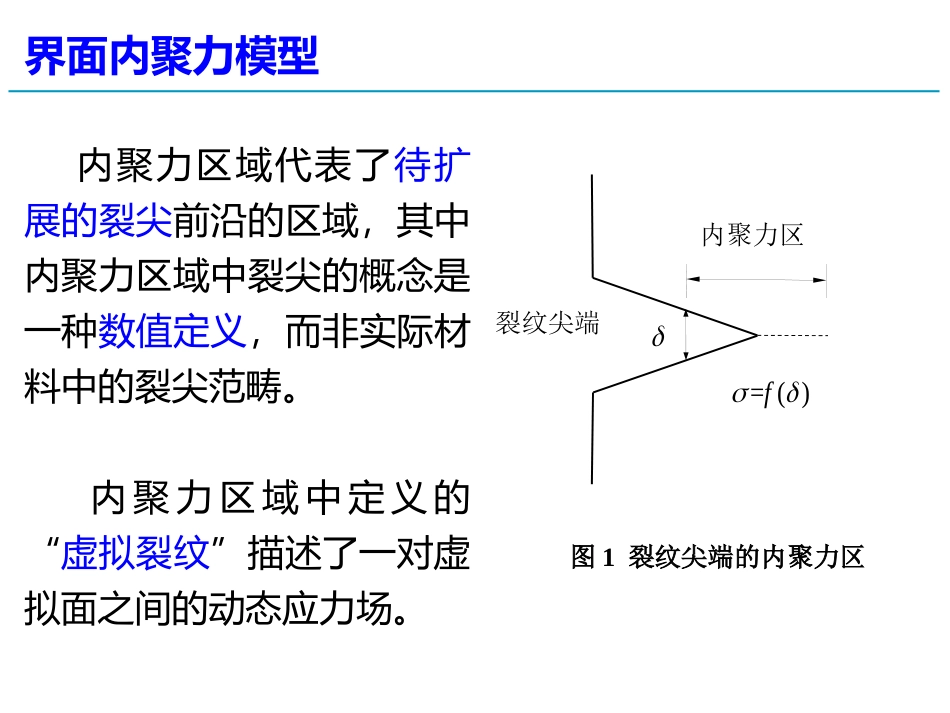
xxxxxxx.xx.xx界面内聚力模型及内聚力有限元法界面内聚力模型随着复合材料结构种类的多样性发展，传统断裂力学已不能满足韧性开裂以及复合材料界面开裂等研究需求。基于弹塑性断裂力学的内聚力模型(cohesivezonemodel,CZM)已被应用于计算复合材料界面损伤和断裂过程。内聚力实际上是物质原子或分子之间的相互作用力。在内聚力区域内，应力是开裂位移的函数，即张力-开裂位移（Traction-separation）关系，也称为内聚力准则。界面内聚力模型内聚力区域代表了待扩展的裂尖前沿的区域，其中内聚力区域中裂尖的概念是一种数值定义，而非实际材料中的裂尖范畴。内聚力区域中定义的“虚拟裂纹”描述了一对虚拟面之间的动态应力场。内聚力区裂纹尖端=()f图1裂纹尖端的内聚力区界面内聚力模型内聚力模型的重要特征是张力-位移曲线的形状和内聚力参数。目前，应用较为广泛的内聚力准则，如图2所示。b)双线性型tc)多项式型td)梯形型a)指数型tt图2不同形式的内聚力准则a)指数b)双线性c)多项式d)梯形区界面内聚力模型双线性张力位移法则双线性张力位移法则是一种简单有效的内聚力法则，被广泛应用于有限元软件中已实现内聚力模型计算。控制方程为max00n0maxn0nfnfnn（）（）max00tt0maxtftfftt（）（）界面内聚力模型maxn0nfnmaxt0tfta)法向张力位移关系b)切向张力位移关系图3双线性张力位移关系其中为法向的应力值，为切向的应力值，、分别为法向及切向的最大应力值，对应的裂纹界面张开位移值分别为。图线斜率为内聚力刚度。maxmax0n0t界面内聚力模型在达到其最大值后应力开始减小至零时裂纹开裂完成，其对应的位移值为最终开裂位移值。各项的断裂能临界值,。计算公式为：fncnctnmaxntmaxt1212cfcf双线性内聚力模型简单有效，能较好的在有限元等方法中计算而一般不会出现计算困难。界面内聚力模型梯形张力位移法则（逐段线性张力位移法则）控制方程为ff2211f2fmaxmax1max0--）（临界的断裂能值为：梯形张力位移关系中，其模型的参数除了最大应力值以及临界断裂能之外，还必须给出的值。12maxc12f图4梯形张力位移）（12maxc21f界面内聚力模型多项式张力位移法则多项式张力位移法则的内聚力模型由Needleman于1992年提出，采用了高次多项式的函数。断裂能的控制方程22000002200027141142321411232nnnttnT为法向与切向刚度之间的一个比例系数，为纯法向时的最大内聚力，为最大张开量。0T0界面内聚力模型由与双线性及梯形张力位移关系不同，多项式张力位移关系为连续性的方程，首先提出断裂能的控制方程，对其进行偏导求得张力位移关系的控制方程。T可得222n000000271214nnnnnTT2200002714ttnrTT界面内聚力模型指数内聚力模型指数内聚力模型被广泛的应用于计算复合材料界面开裂、脆性材料中的动态裂纹扩展、韧性基体上薄膜涂层之间的开裂裂纹萌生等过程。指数内聚力模型具有连续性的张力位移关系,同时其断裂能的值也为连续变化。与双线性以及梯形法则相比，指数法则的张力位移关系是非线性连续变化的，更符合实际界面开裂的状态。界面内聚力模型指数内聚力模型在开裂过程中的断裂能控制方程为:、分别为界面上的法向与切向位移值，为纯法向开裂状态下界面完全开裂时的界面断裂能，、为法向与切向界面开裂特征位移，即应力最大值点对应的位移值。+ntnnt参数，分别...