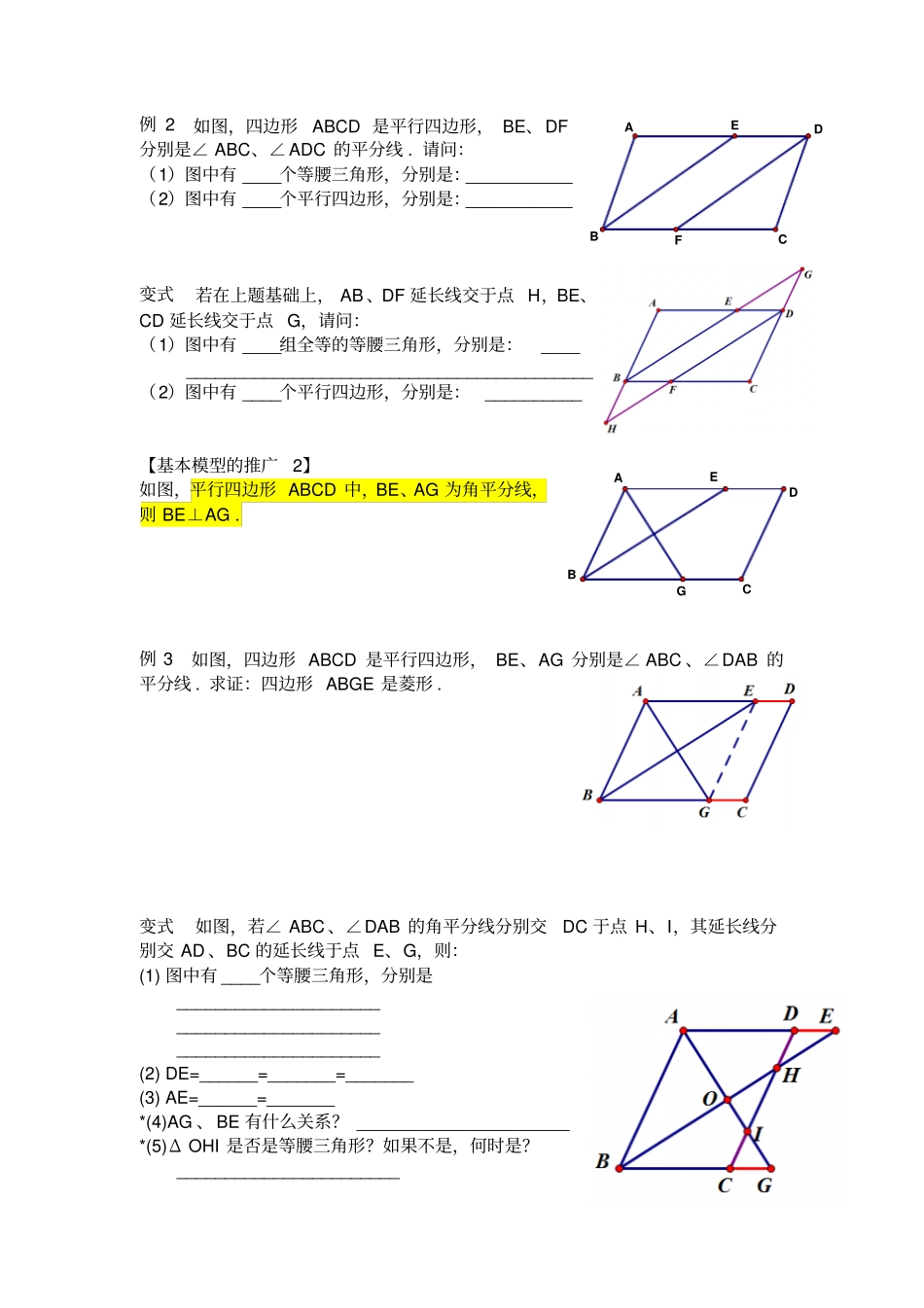
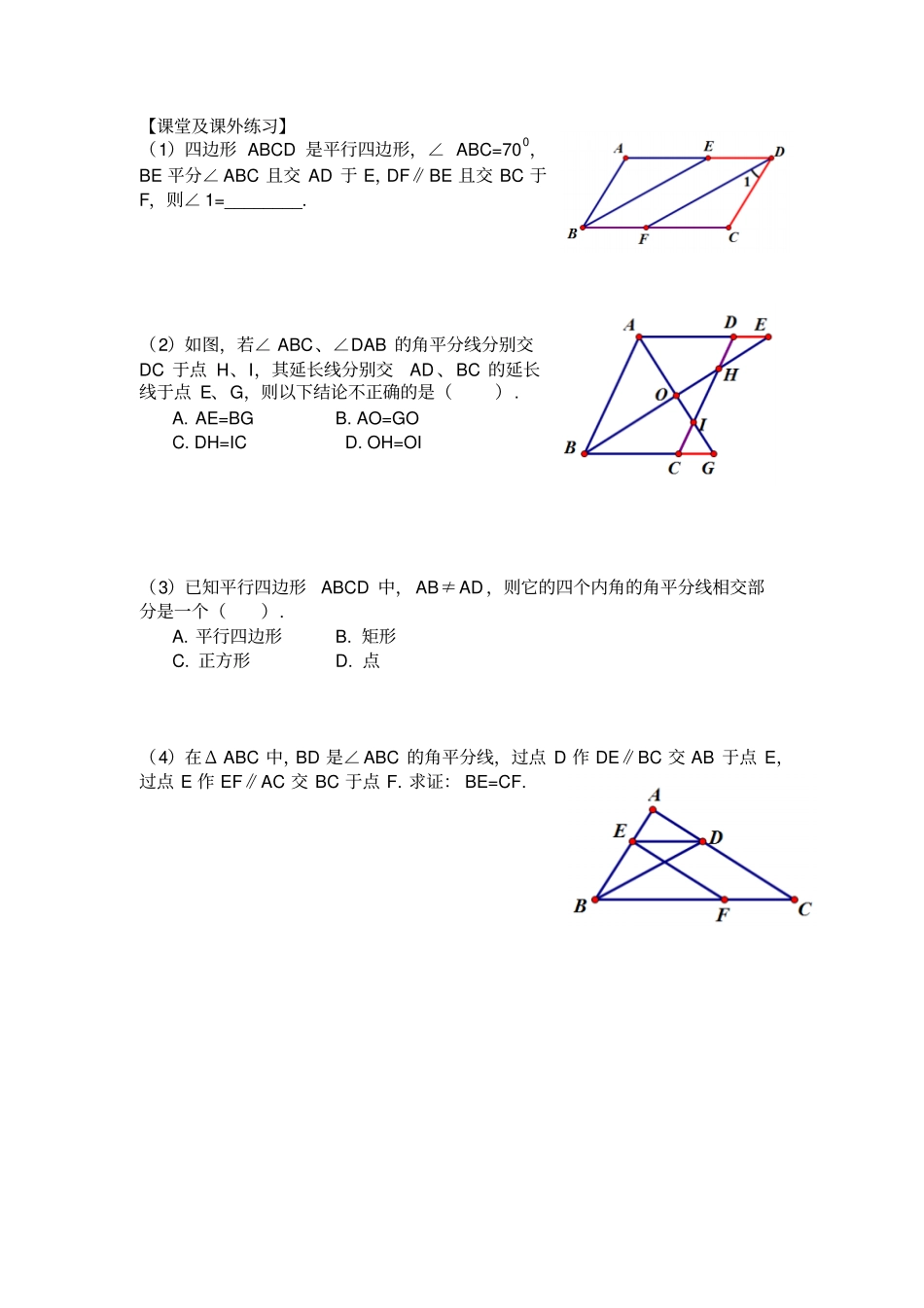
角平分线在平行四边形中的应用(学案)班别:姓名:【基本模型】如图,平行四边形ABCD 中, BE 为角平分线,则 AB=AE. 证明: BE 为∠ ABC 的平分线∴___________ 四边形 ABCD 是平行四边形∴___________ ∴___________ ∴___________ ∴AB=AE 例 1 如图,四边形 ABCD 是平行四边形, BE 平分∠ ABC 且交 AD 于点 E,求证: ED+DC=BC. 变式 1 如图,四边形ABCD 是平行四边形, BE 平分∠ABC 且交 AD 延长线于 E,你可以得到什么结论?你知道为什么吗?答:(1)图中有 __个等腰三角形,分别是:______________ (2)ED、BC 和 DC 的等量关系:__________________ 变式 2 如图,四边形 ABCD 是平行四边形, BE 平分∠ ABC 且恰好经过点 D,你又可以得到什么结论?你知道为什么吗?答:(1)图中有 __个等腰三角形,分别是:___________ (2)ED、BC 和 DC 的等量关系:_______________ (3)四边形 ABCD 是_________ 【基本模型的推广1】如图,平行四边形ABCD 中, BE、DF 为角平分线,则 BE∥DF. 321ECADBFECADB例 2 如图,四边形ABCD 是平行四边形, BE、DF分别是∠ ABC、∠ ADC 的平分线 . 请问:(1)图中有 ____个等腰三角形,分别是:___________ (2)图中有 ____个平行四边形,分别是:___________ 变式若在上题基础上, AB 、DF 延长线交于点 H,BE、CD 延长线交于点 G,请问:(1)图中有 ____组全等的等腰三角形,分别是:____ __________________________________________ (2)图中有 ____个平行四边形,分别是:__________ 【基本模型的推广2】如图,平行四边形 ABCD 中,BE、AG 为角平分线,则 BE⊥AG . 例 3 如图,四边形 ABCD 是平行四边形, BE、AG 分别是∠ ABC 、∠DAB 的平分线 . 求证:四边形 ABGE 是菱形 . 变式如图,若∠ ABC 、∠DAB 的角平分线分别交DC 于点 H、I,其延长线分别交 AD 、BC 的延长线于点 E、G,则:(1) 图中有 ____个等腰三角形,分别是_____________________ _____________________ _____________________ (2) DE=______=_______=_______ (3) AE=______=_______ *(4)AG 、 BE 有什么关系? ______________________ *(5)Δ OHI 是否是等腰三角形?如果不是,何时是?_______________________ GECADBFECADB【课堂及课外练习】(1)四边形 ABCD 是平行四...