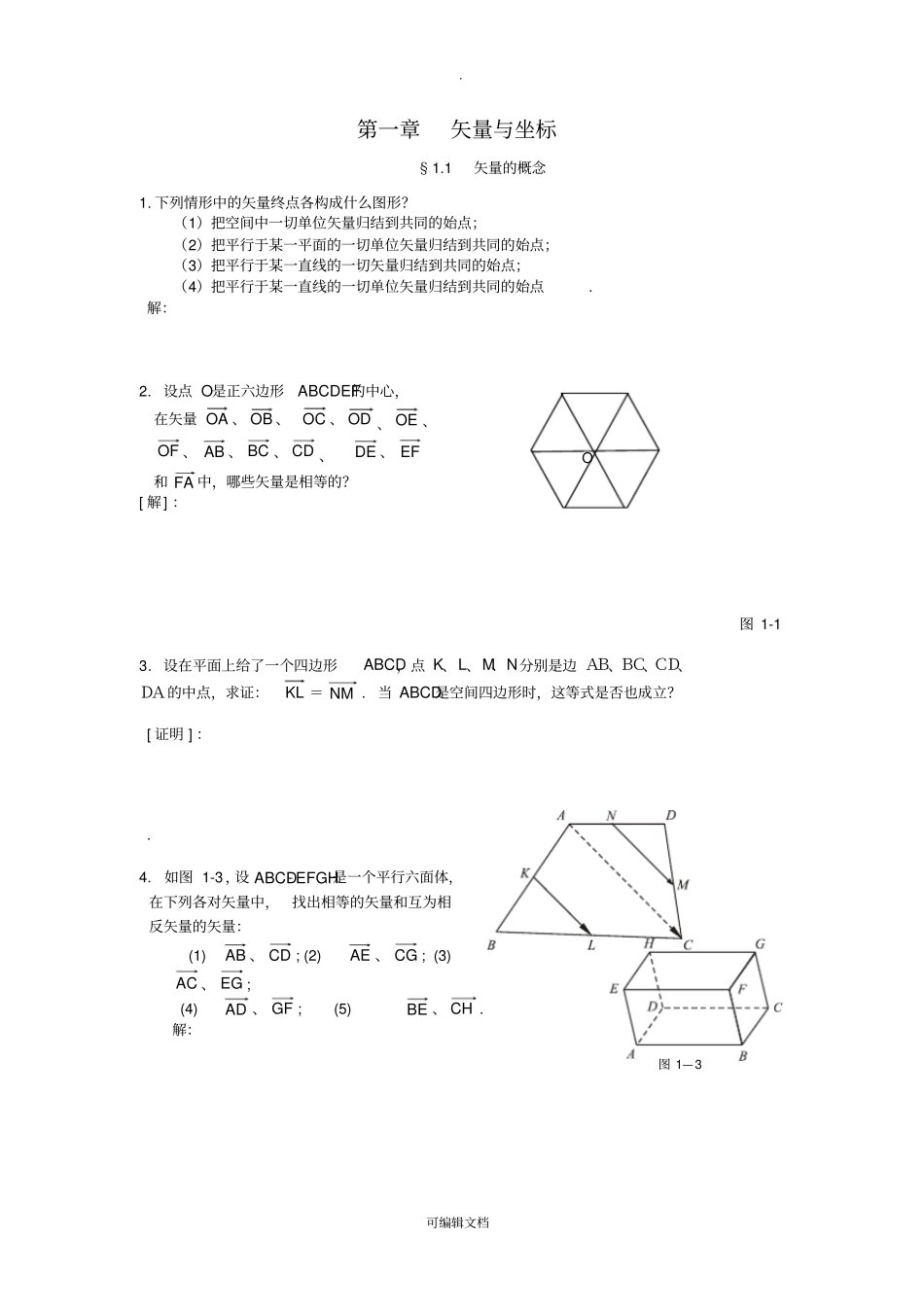
. 可编辑文档第一章矢量与坐标§1.1 矢量的概念1. 下列情形中的矢量终点各构成什么图形?(1)把空间中一切单位矢量归结到共同的始点;(2)把平行于某一平面的一切单位矢量归结到共同的始点;(3)把平行于某一直线的一切矢量归结到共同的始点;(4)把平行于某一直线的一切单位矢量归结到共同的始点. 解:2. 设点 O是正六边形ABCDEF的中心,在矢量 OA 、 OB 、OC 、 OD 、 OE 、OF 、 AB 、 BC 、 CD 、DE 、 EF和 FA 中,哪些矢量是相等的?[ 解] :图 1-13. 设在平面上给了一个四边形ABCD,点 K、L、M、N分别是边 AB、BC、CD、DA的中点,求证:KL = NM . 当 ABCD是空间四边形时,这等式是否也成立?[ 证明 ] :. 4. 如图 1-3 ,设 ABCD- EFGH是一个平行六面体,在下列各对矢量中,找出相等的矢量和互为相反矢量的矢量:(1) AB 、 CD ; (2) AE 、 CG ; (3) AC 、 EG ; (4) AD 、 GF ; (5) BE 、 CH . 解:图 1—3 O . 可编辑文档§1.2 矢量的加法1. 要使下列各式成立,矢量ba,应满足什么条件?(1);baba(2);baba(3);baba(4);baba(5).baba解:§1.3 数量乘矢量1 试解下列各题.⑴ 化简)()()()(bayxbayx.⑵ 已知3212eeea,321223eeeb,求ba,ba和ba23.⑶ 从矢量方程组byxayx3243,解出矢量 x , y .解: 2 已知四边形ABCD 中,caAB2,cbaCD865,对角线 AC 、 BD 的中点分别为 E 、 F ,求 EF .解: 3 设baAB5,baBC82,)(3baCD,证明: A、 B 、 D 三点共线.解:. 可编辑文档 4 在四边形 ABCD 中,baAB2,baBC4,baCD35,证明 ABCD为梯形.解:6. 设 L、M、N分别是Δ ABC的三边 BC、CA、AB的中点,证明:三中线矢量AL , BM , CN可 以构成一个三角形.7. 设 L、M、 N是△ ABC的三边的中点,O是任意一点,证明OBOA+OC = OL +OM +ON .解:8. 如图 1-5 ,设 M是平行四边形ABCD的中心, O是任意一点,证明OA +OB +OC +OD =4OM .解:9 在 平 行 六 面 体 ABCDEFGH( 参 看 第 一 节 第4题 图 ) 中 , 证 明AGAHAFAC2.证明:. 10. 用矢量法证明梯形两腰中点连续平行于上、下两底边且等于它们长度和的一半.解11. 用矢量法证明,平行四边行的对角线互相平分. 解图 1-4 . 可编辑文档12. 设点 O是平面上正多边形A1A2⋯An的中心,证明 :1OA +2OA +...