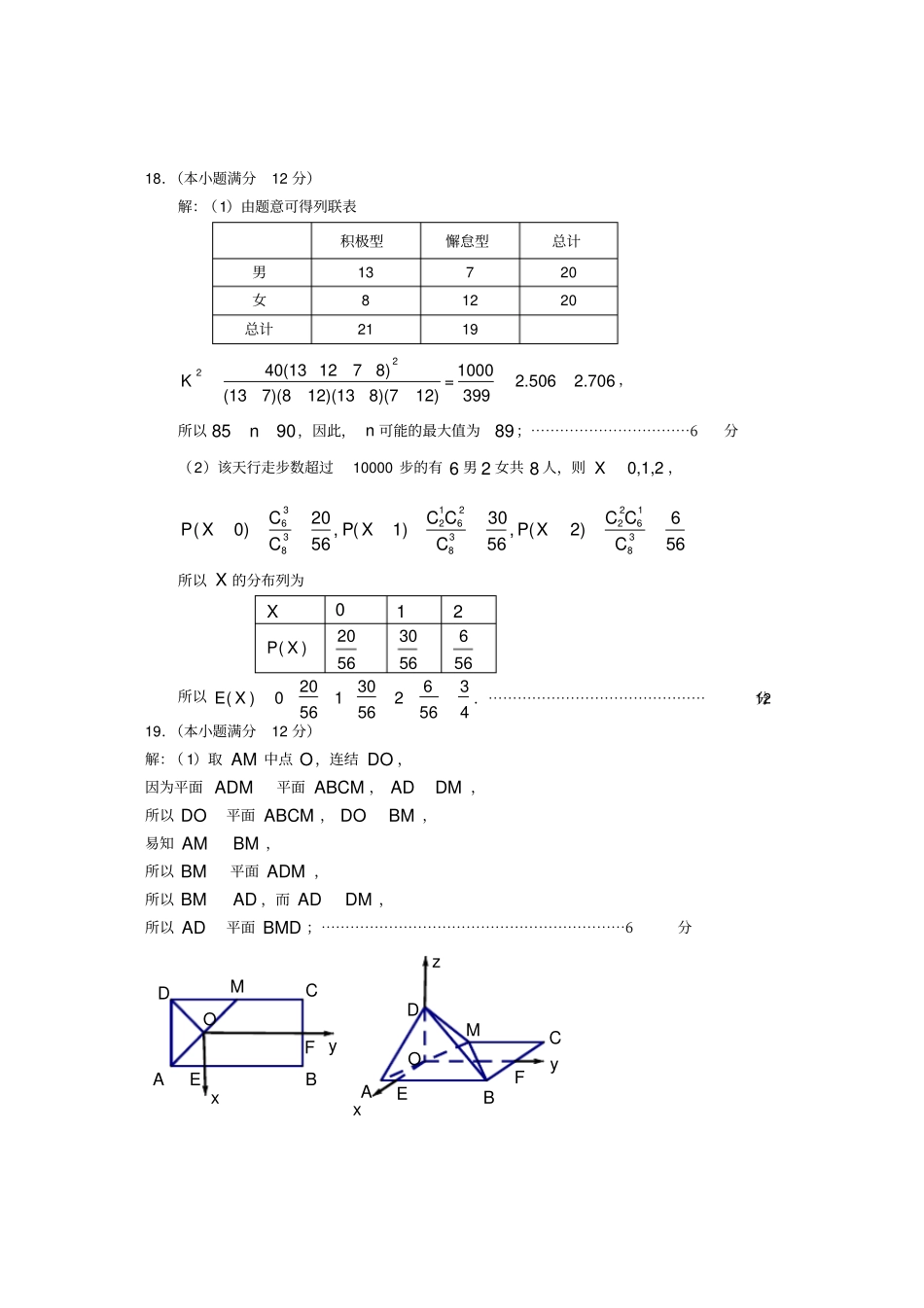
贵阳市 2019 年高三适应性考试(一)理科数学参考答案与评分建议一、选择题 : 本大题共12 小题,每小题5 分,在每小题给出的四个选项中,只有一项是符合题目要求的。题号123456789101112答案DACAABABBCDC二、填空题:本大题共4 小题,每小题5 分。13. 40; 14.31 ; 15.2, 2; 16.34, 8 3三、解答题:解答应写出文字说明,证明过程或演算步骤。17.(本小题满分12 分)解:( 1)由正弦定理得:BCCBAsinsincossinsin,即BCCBCBsinsincossinsin)(,故BCCBsinsinsincos,因为0sinC,所以BBsincos,因为B0,所以4B;⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯6分(2)因为cba,,成等比数列,所以acb2,由余弦定理得acBaccacos222,由重要不等式知22cosacacBac≤,所以1coscos23B≥,因为B0,且函数xycos在 (0,) 上是减函数,所以3B ≤. ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯12 分18.(本小题满分12 分)解:(1)由题意可得列联表积极型懈怠型总计男13720女81220总计21192240(13 1278)1000=2.5062.706(137)(812)(138)(712)399K,所以 8590n,因此, n 可能的最大值为89;⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯6分(2)该天行走步数超过10000 步的有 6 男 2 女共 8 人,则0,1,2X,312216262633388820306(0),(1),(2)565656CC CC CP XP XP XCCC所以 X 的分布列为X012()P X20563056656所以203063()0125656564E X.⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯12分19.(本小题满分12 分)解:( 1)取 AM 中点 O,连结 DO ,因为平面 ADM平面 ABCM ,DMAD,所以 DO平面 ABCM ,BMDO,易知BMAM,所以 BM平面 ADM ,所以ADBM,而DMAD,所以 AD平面 BMD ;⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯6分FEOEOMADBCABCMDzyxyxF(2)如图,以 O为原点建立空间直角坐标系,( x 轴垂直 AB 交 AB 于 E , y 轴垂直 BC交 BC 于 F , OD 为 z 轴)则11(,,0)22A,1 3(,,0)2 2B1 3(,,0)2 2C,2(0,0,)2D,1 1(,,0)2 2M所以1 32( 1,0,0),(,,)2 22BCDCuuuruuur,设1=( , , )x y zn是平面 BCD 的一个法向量,则1100BCDCuuuruuurnn,所以000 1320222xyzxyz,令2z,解得0x,23y,即11222=(0,,2),||33nn,由( 1)知 ADuuur是平面 MBD 的一个法向量,且1 12(,),|| 12 2 2ADADuuuruuur1111012 223cos,==11|| ||2213ADADADuuuruuuruuurnnn,又因为...