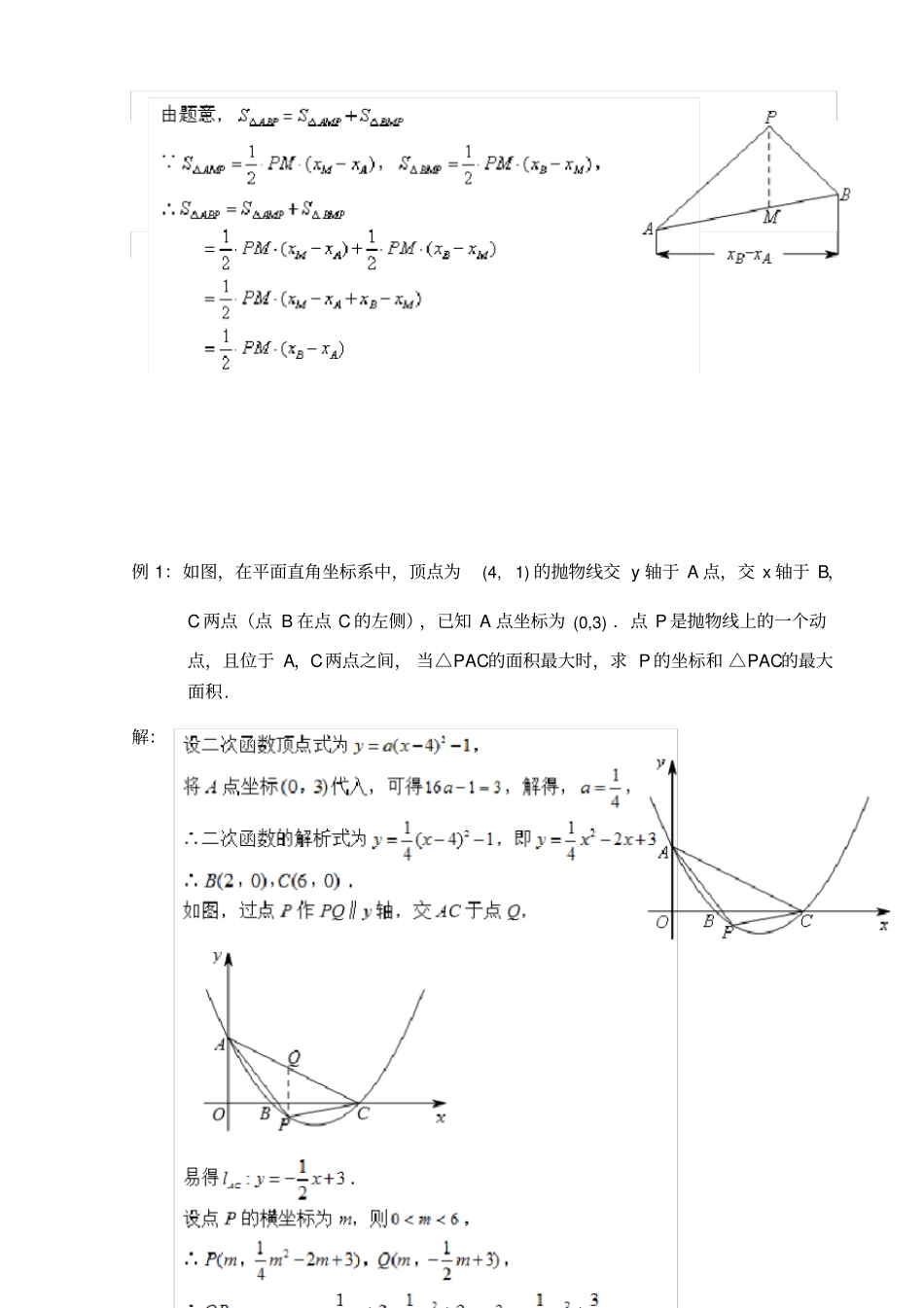
二次函数三角形之面积问题(铅垂法)专题前请先思考以下问题 :问题 1:坐标系背景下问题的处理原则是什么问题 2:坐标系中处理面积问题的思路有哪些问题 3:具有什么样特征的三角形在表达面积时会使用铅垂法问题 4:铅垂法的具体做法是什么问题 5:如何利用铅垂法表达三角形的面积以下是问题及答案,请对比参考:问题 1:坐标系背景下问题的处理原则是什么答:充分利用横平竖直线段长,几何特征函数特征互转。问题 2:坐标系中处理面积问题的思路有哪些答:公式法(规则图形);割补法(分割求和,补形作差);转化法(例:同底等高)。问题 3:具有什么样特征的三角形在表达面积时会使用铅垂法答:三边均是斜放置在坐标系中的三角形在表达面积时一般使用铅垂法。问题 4:铅垂法的具体做法是什么答:若是固定的三角形,则可从任意一点作铅垂;若为变化的图形,则从动点向另外两点所在的定直线作铅垂。问题 5:如何利用铅垂法表达三角形的面积答:从动点向另外两点所在的固定直线作铅垂,将变化的竖直线段作为三角形的底,则高就是两个定点的横坐标之差,然后结合三角形的面积公式表达。例 1:如图,在平面直角坐标系中,顶点为(4,1) 的抛物线交 y 轴于 A 点,交 x 轴于 B,C 两点(点 B 在点 C 的左侧),已知 A 点坐标为 (0,3) .点 P 是抛物线上的一个动点,且位于 A,C两点之间, 当△PAC的面积最大时,求 P 的坐标和 △PAC的最大面积. 解:试题难度: 三颗星 知识点: 铅垂法求面积(铅垂线在三角形内部)例 2:如图,一次函数122yx与 y 轴、 x 轴分别交于点 A,B,抛物线2yxbxc过 A,B 两点.Q 为直线 AB下方的抛物线上一点,设点Q 的横坐标为 n,△QAB的面积为 S,求出 S与 n 之间的函数关系式并求出S的最大值 .解:试题难度: 三颗星 知识点: 铅垂法求面积(铅垂线在三角形外部)⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯总结反思篇:决胜中考 :1.如图,在平面直角坐标系中,二次函数213222yxx的图象与 y 轴交于点 A,与 x轴交于 B,C 两点(点 B 在点 C的左侧).点 P 是第二象限内抛物线上的点,△PAC的面积为 S,设点 P 的横坐标为 m,求 S与 m 之间的函数关系式 .2. 如图,已知抛物线213222yxx与 x 轴交于 A,B 两点,与 y 轴交于点 C.M 为抛物线上一动点,且在第三象限,若存在点M 使得12ACMABC...