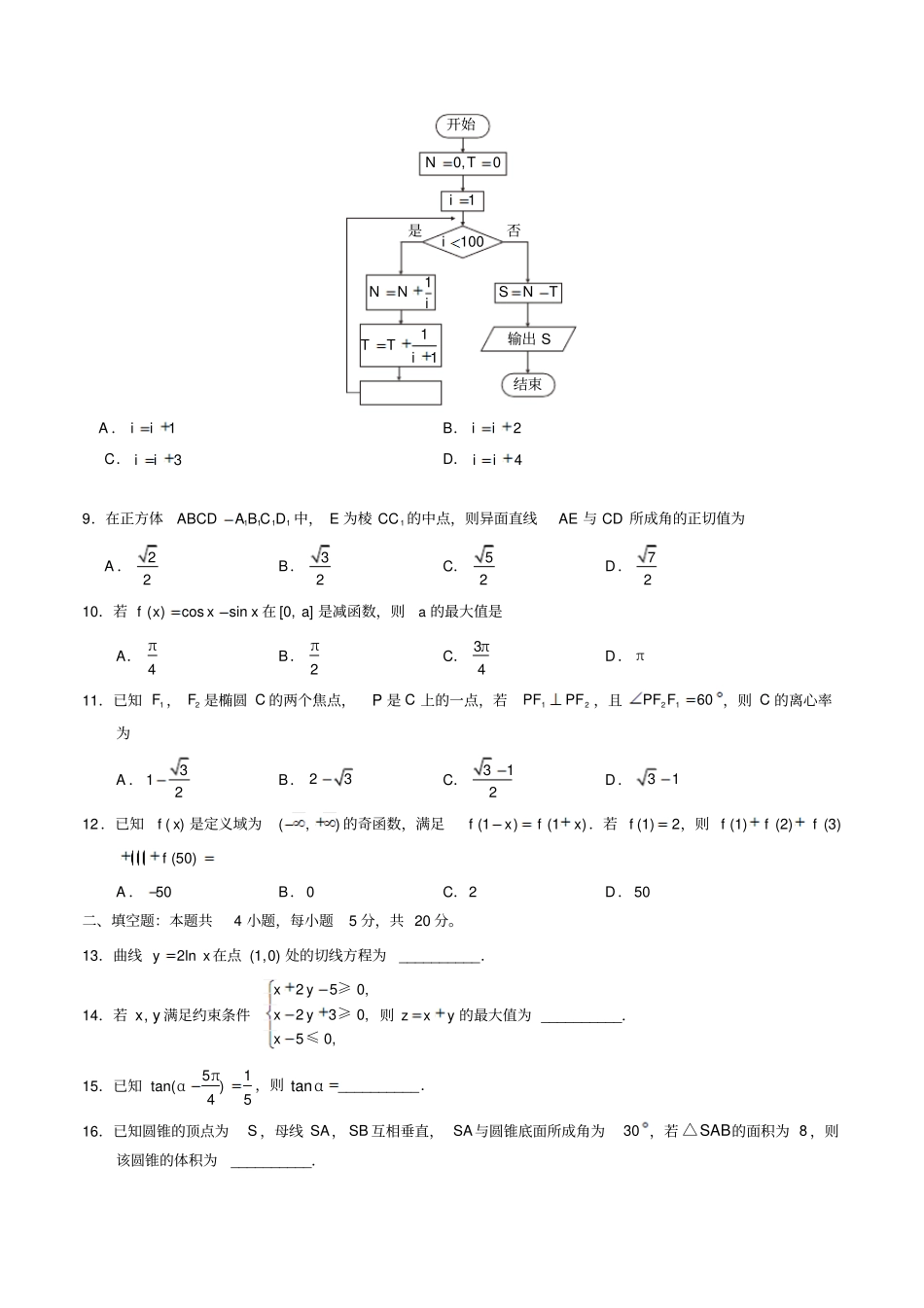
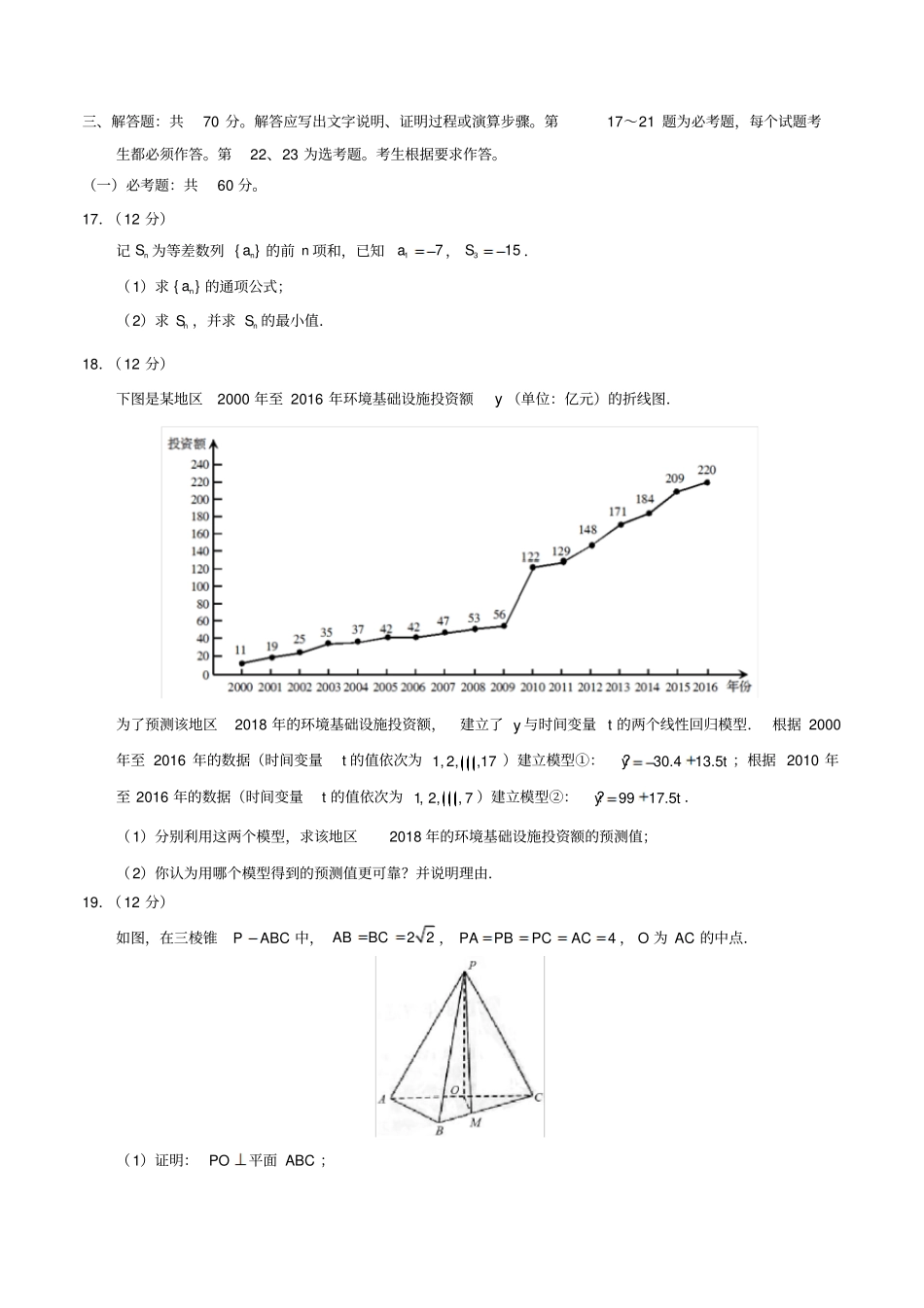
2018 年普通高等学校招生全国统一考试文科数学一、选择题:本题共12 小题,每小题5 分,共 60 分,在每小题给出的四个选项中,只有一项是符合题目要求的。学 @科网1. i 23iA. 32iB. 32iC.32iD.32i2.已知集合1,3,5,7A,2,3,4,5B,则 ABA. 3B. 5C. 3,5D. 1,2,3,4,5,73.函数2eexxfxx的图像大致为4.已知向量a , b 满足 ||1a,1a b,则(2)aabA .4 B.3 C.2 D.0 6.双曲线22221(0,0)xyabab的离心率为3 ,则其渐近线方程为A .2yxB.3yxC.22yxD.32yx7.在ABC△中,5cos25C,1BC,5AC,则 ABA . 4 2B.30C.29D. 2 58.为计算11111123499100S,设计了如图的程序框图,则在空白框中应填入A .1iiB.2iiC.3iiD.4ii9.在正方体1111ABCDA B C D 中, E 为棱1CC 的中点,则异面直线AE 与 CD 所成角的正切值为A .22B.32C.52D.7210.若( )cossinf xxx 在 [0,]a 是减函数,则a 的最大值是A. π4B. π2C. 3π4D. π11.已知1F ,2F 是椭圆 C 的两个焦点,P 是 C 上的一点,若12PFPF ,且2160PF F,则 C 的离心率为A .312B. 23C.312D.3112 .已知( )f x 是定义域为(,) 的奇函数,满足(1)(1)fxfx .若(1)2f,则(1)(2)(3)fff(50)fA .50B.0 C.2 D.50 二、填空题:本题共4 小题,每小题5 分,共 20 分。13.曲线2lnyx 在点 (1,0) 处的切线方程为__________.14.若,x y 满足约束条件250,230,50,xyxyx≥≥≤则 zxy 的最大值为 __________.15.已知5π1tan()45α,则 tanα__________.16.已知圆锥的顶点为S ,母线 SA, SB 互相垂直, SA与圆锥底面所成角为30 ,若SAB△的面积为 8 ,则该圆锥的体积为__________.开始0,0NTSNTS输出1i100i1NNi11TTi结束是否三、解答题:共70 分。解答应写出文字说明、证明过程或演算步骤。第17~21 题为必考题,每个试题考生都必须作答。第22、23 为选考题。考生根据要求作答。(一)必考题:共60 分。17.(12 分)记nS 为等差数列 {}na的前 n 项和,已知17a,315S.(1)求 {}na的通项公式;(2)求nS ,并求nS 的最小值.18.(12 分)下图是某地区2000 年至 2016 年环境基础设施投资额y (单位:亿元)的折线图.为了预测该地区2018 年的环境基础设施投资额,建立了 y 与时间变量 t 的两个线性回归模型. 根据 2000年至 2016 年的数据(时间变量t 的值依次...