地图投影方位投影VIP免费

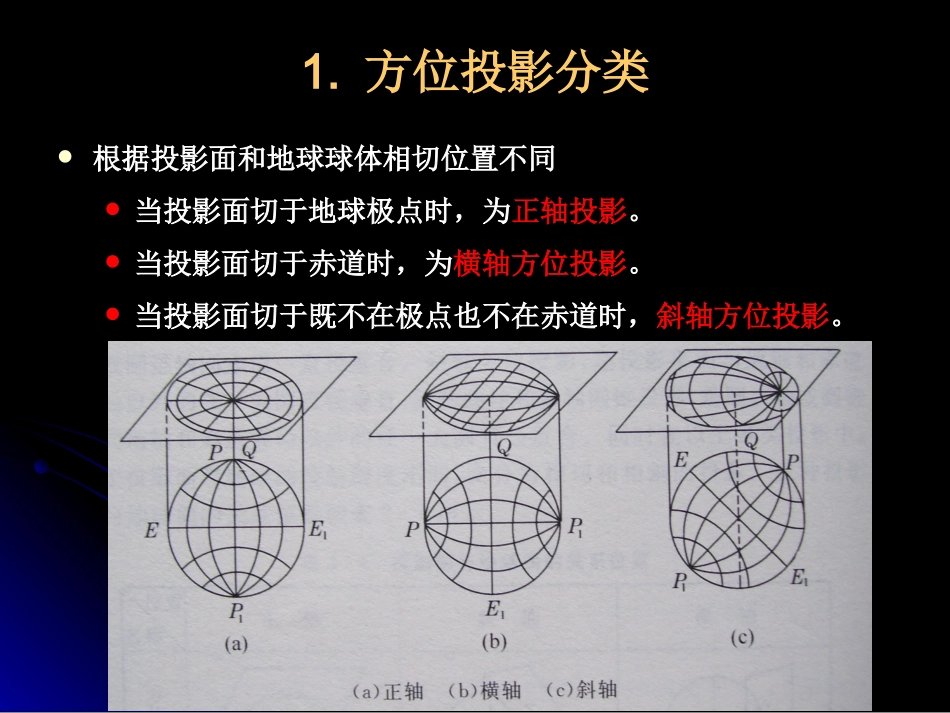
第三章方位投影第三章方位投影3.1方位投影的种类和基本原理3.2等面积方位投影3.3等距离方位投影3.4透视方位投影的种类和一般公式3.5正射投影3.6球面投影（等角方位投影）3.7球心投影（日晷投影）3.8方位投影的分析和应用第三章方位投影第三章方位投影一、一、方位投影的种类和基本原理方位投影的种类和基本原理概念：方位投影是以平面作为投影面，使平面与地球表面相切或相割，将球面上的经纬线投影到平面上所得到的图形。投影平面上，由投影中心（平面与球面相切的点，或平面与球面相割的割线圆心点）向各个方向的方位角与实地相等，等变形线是以投影中心为圆心的同心圆，切点或相割的割线无变形。适合制作形状大致为圆形区域的地图。1.1.方位投影分类方位投影分类根据投影面和地球球体相切位置不同当投影面切于地球极点时，为正轴投影。当投影面切于赤道时，为横轴方位投影。当投影面切于既不在极点也不在赤道时，斜轴方位投影。22、正轴方位投影、正轴方位投影投影中心为极点，纬线为同心圆，经线为同心圆的半径，两条经线间的夹角与实地相等。等变形线都是以投影中心为圆心的同心圆。包括等角、等积、等距三种变形性质，主要用于制作两极地区图。''1ADdADRdZ面积变形为最大角度变形为:m和n分别是经纬线长度比二二..等面积方位投影等面积方位投影等面积投影的条件为:0因此有:因此有:对上式积分得:因为当Z=0时开方得:00二二..等面积方位投影等面积方位投影0最大角度变形值为:因此长度比公式为:面积比为:P=1由于secZ＞cosZ,因此00等面积方位投影为兰勃特于1772年所创,故又称为兰勃特等面积方位投影.二二..等面积方位投影等面积方位投影横轴方位投影——等积变形分布规律投影中心无变形，离开投影中心愈远角度、长度变形增大。经纬线形式中央经线为直线，其它经线是对称于中央经线的凹向曲线；中央纬线为直线，其它纬线是对称于中央纬线的凸向曲线。在中央经线上纬线间隔自投影中心向外逐渐减小。在中央纬线上经线间隔自投影中心向东、向西方向逐渐减小。斜轴方位投影——等积变形分布规律投影中心无变形，离开投影中心愈远角度、长度变形增大。经纬线形式中央经线为直线，其它经纬线均是曲线。在中央经线上纬线间隔自投影中心向外逐渐减小。三三..等距方位投影等距方位投影等距离条件为:因此有:因为Z=0时ρ=0,最大角度变形值为:此投影为波斯托于1581年所创.又称波斯托投影。三三..等距方位投影等距方位投影三三..等距方位投影等距方位投影等距方位投影属于任意投影，它既不等积也不等角。投影后经线保持正长，经线上纬距保持相等。纬线投影后为同心圆，经线投影为交于纬线圆心的直线束，经线投影后保持正长，所以投影后的纬线间距相等。经纬线投影后正交，经纬线方向为主方向。角度、面积等变形线为以投影中心为圆线的同心圆。球面上的微圆投影为椭圆，且误差椭圆的长半径和纬线方向一致，短半径与经线方向一致，且等于微圆半径r，又因自投影中心，纬线扩大程度越来越大，所以变形椭圆的长半径也越来越长，椭圆越来越扁。常用来做两极的投影。横轴方位投影——等距变形分布规律投影中心无变形，离开投影中心愈远角度、长度变形增大，面积变形、角度变形都不大。经纬线形状中央经线为直线，其它经线是对称于中央经线的曲线。中央纬线为直线，其它纬线是对称于中央纬线的曲线。在中央经线上纬线间隔相等。在中央纬线上经线间隔相等。斜轴方位投影——等距变形分布规律投影中心无变形，离开投影中心愈远角度、长度变形增大，面积变形、角度变形都不大。经纬线形式中央经线为直线，其它经纬线均是曲线。在中央经线上纬线间隔相等。四四..透视方位投影透视方位投影1234透视方位投影可以分为(1)正射投影(2)外心投影(3)球面投影(4)球心投影并根据投影面与地球面的不同关系可以分成:正轴、斜轴和横轴投影。四四..透视方位投影透视方位投影1234ZA′sincosLRZDRZ带入上式:P四四..透视方位投影透视方位投影1234由此得到直角坐标公式为:变形公式为:...