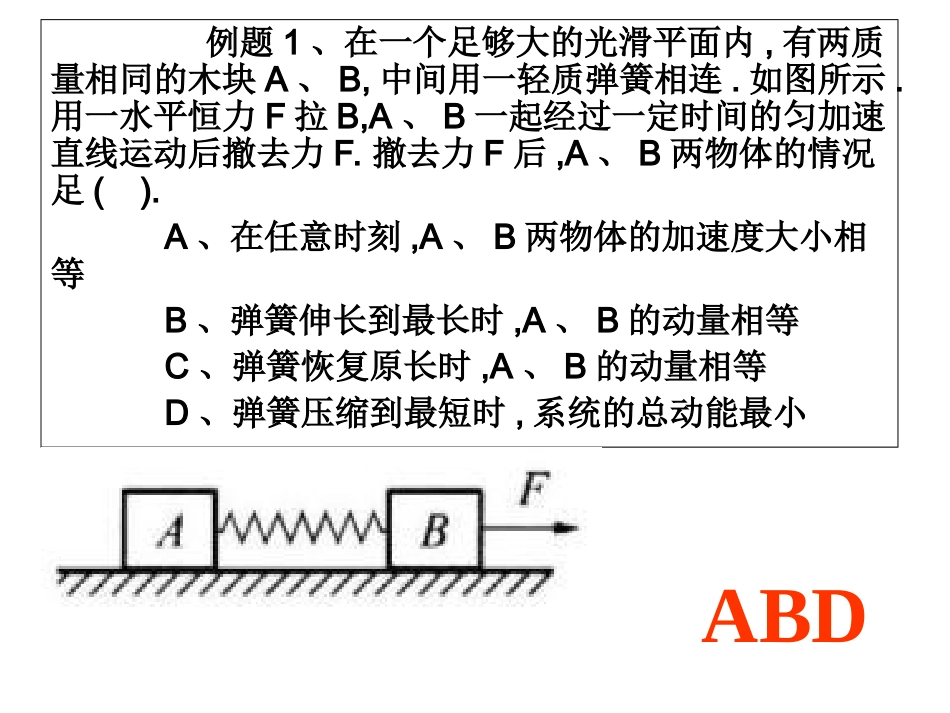
碰撞模型的扩展一、注意:状态的把握由于弹簧的弹力随形变量变化,弹簧弹力联系的“两体模型”一般都是作加速度变化的复杂运动,所以通常需要用“动量关系”和“能量关系”分析求解。复杂的运动过程不容易明确,特殊的状态必须把握:弹簧最长(短)时两体的速度相同;弹簧自由时两体的速度最大(小)。一、碰撞中弹簧模型----------弹簧弹力联系的“两体模型”V0BA例题1、在一个足够大的光滑平面内,有两质量相同的木块A、B,中间用一轻质弹簧相连.如图所示.用一水平恒力F拉B,A、B一起经过一定时间的匀加速直线运动后撤去力F.撤去力F后,A、B两物体的情况足().A、在任意时刻,A、B两物体的加速度大小相等B、弹簧伸长到最长时,A、B的动量相等C、弹簧恢复原长时,A、B的动量相等D、弹簧压缩到最短时,系统的总动能最小ABD例3.质量均为m的A、B两球,一轻弹簧连接后放在光滑水平面上,A被一水平速度为v0,质量为m/4的泥丸P击中并粘合,求损失的机械能和弹簧能具有的最大势能。解析:如上分析图,整个过程有三部分组成:(1)P与A作用获瞬间速度。(2)P与A一起运动后于弹簧作用再与B作用,P与A减速运动,B加速运动。(3)当P、A、B有共同速度时,弹簧有最大压缩量,具有EPmax;从状态1状态2有动量守恒:v0=(+m)v1得v1=1/5v0①从状态2状态3有动量守恒:(m/4+m)v1=(m+m/4+m)v2②(或从状态1状态3有动量守恒:m/4v0=(m+m/4+m)v2所损失的机械能在过程1-2中,设为E减。E减=1/2·m/4·v02-1/2(m/4+m)v12=1/10mv02③由能量守恒得:弹簧具有的最大弹性势能为EP1/2·(m/4+m)·v12=1/2·(m+m/4+m).v22+EP④由①-④得:EP=4m920mv4m例题4.用轻弹簧相连的质量均为2kg的A、B两物块都以的速度在光滑的水平地面上运动,弹簧处于原长,质量为4kg的物体C静止在前方,如图3所示,B与C碰撞后二者粘在一起运动。求:在以后的运动中(1)当弹簧的弹性势能最大时物体A的速度多大?(2)弹性势能的最大值是多大?(3)A的速度有可能向左吗?为什么?•(1)当A、B、C三者的速度相等时弹簧的弹性势能最大,由于A、B、C三者组成的系统动量守恒,有ACBABAv)mmm(v)mm(smvA/3'v(2)B、C碰撞时B、C组成的系统动量守恒,设碰后瞬间B、C两者速度为smvvmmvmCBB/2'')(,三物块速度相等为vA时弹簧的弹性势能最大为EP,根据能量守恒JvmmmvmvmmEACBAACBP12)(2121')(21222由系统动量守恒得BCBAABAvmmvmvmvm)(设A的速度方向向左0AvsmvB/4则则作用后A、B、C动能之和JvmmvmEBCBAAk48)(212122系统的机械能JvmmmEEACBAP48)(21'2故A不可能向左运动练习2:如图所示,质量为m的小物体B连着轻弹簧静止于光滑水平面上,质量为2m的小物体A以速度v0向右运动,则(1)当弹簧被压缩到最短时,弹性势能Ep为多大?(2)若小物体B右侧固定一挡板,在小物体A与弹簧分离前使小物体B与挡板发生无机械能损失的碰撞,并在碰撞后立即将挡板撤去,则碰撞前小物体B的速度为多大,方可使弹性势能最大值为2.5Ep?V0BA拓展、在光滑水平面上有一质量m1=20kg的小车,通过一根不可伸长的轻绳与另一质量为m2=5kg的拖车相连接,拖车的平板上放一质量为m3=15kg的物体,物体与平板间的动摩擦因数为μ=0.2.开始时拖车静止,绳没有拉紧,如图所示,当小车以v0=3m/s的速度前进后,带动拖车运动,且物体不会滑下拖车,求:(1)m1、m2、m3最终的运动速度;(2)物体在拖车的平板上滑动的距离。解析:在水平方向上,由于整个系统在运动过程中解析:在水平方向上,由于整个系统在运动过程中不受外力作用,不受外力作用,故故m1m1、、m2m2、、m3m3所组成的系统动量守恒,最终三者所组成的系统动量守恒,最终三者的速度相同(设为的速度相同(设为vv)则)则vmmmvm)(32101)/(5.1smv欲求m3在m2上的位移,需知m1与m2作用后m2的速度,当m1与m2作用时,m3通过摩擦力与m2作用,只有m2获得速度后m3才与m2作用,因此在m1与m2作用时,可以不考虑m3的作用,故m1和m2组成的系统动量也守恒。)/(4.2)(2101''2101smmmvmvvmmvm•mm33在在mm22上移动的距离为上移动的距离为LL,以三物体为...