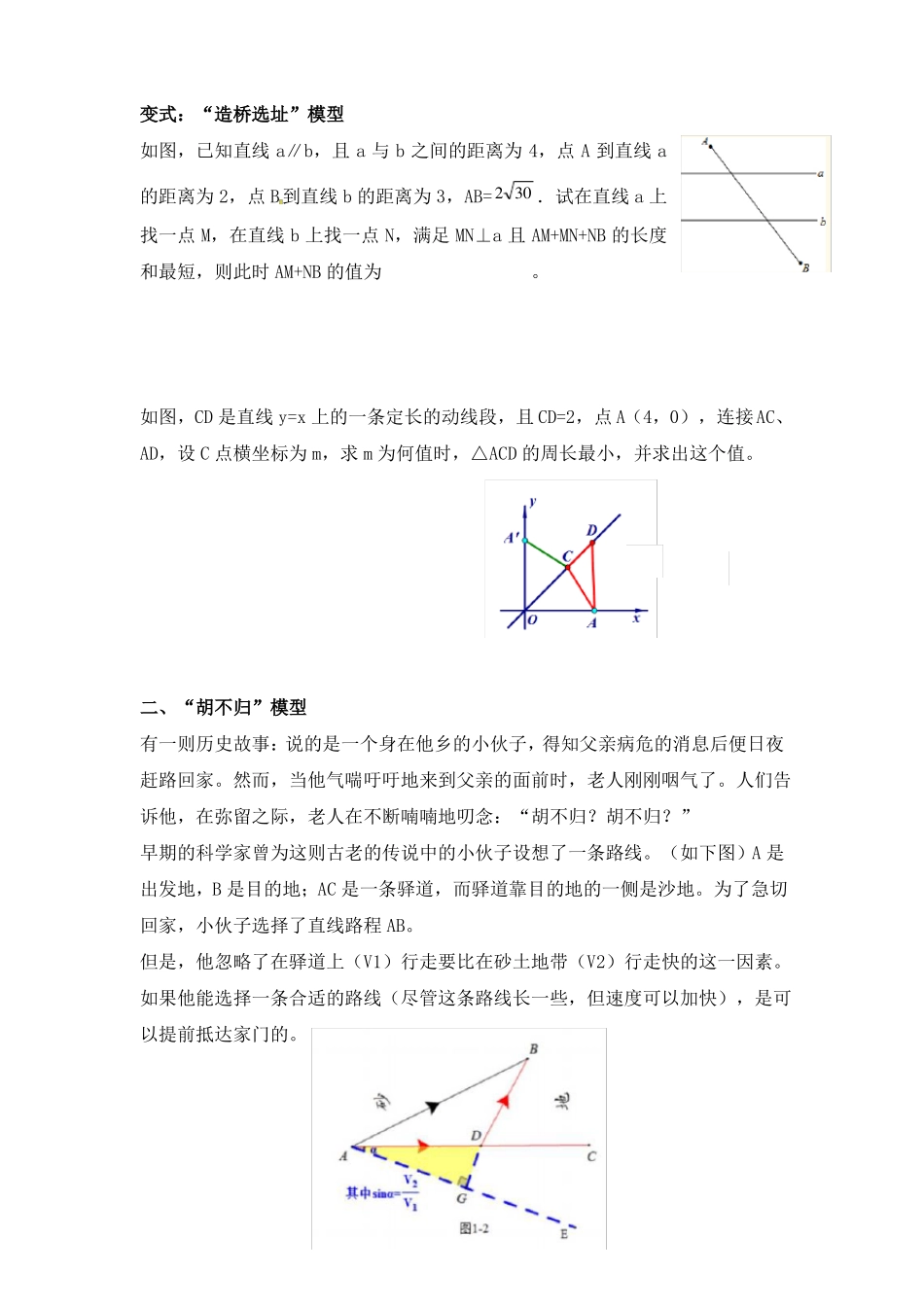
中考压轴专题:“PA+k·PB”型的最值问题当 k 值为 1 时,即可转化为“PA+PB”之和最短问题,就可用我们常见的“将军饮马”模型来处理,即可以转化为轴对称问题来处理。当 k 取任意不为 1 的正数时,通常以动点 P 所在图像的不同来分类,一般分为 2类研究。其中点 P 在直线上运动的类型称之为“胡不归”问题;点 P 在圆周上运动的类型称之为“阿氏圆”问题。一、“将军饮马”模型“将军饮马”:把河岸看作直线 L,先取 A(或 B)关于直线 L的对称点 A′(或 B′),连接A′B(或 B′A),并与直线交于一点 P,则点 P 就是将军饮马的地点,即 PA+PB 即为最短路线。如图,在锐角△ABC 中,AB=4,∠BAC=45°,∠BAC 的平分线交 BC于点 D,M、N 分别是 AD 和 AB 上的动点,则 BM+MN 的最小值是。1如图,在矩形 ABCD 中,AB=10,AD=6,动点 P 满足 S△PAB= 3 S 矩形 ABCD,则点 P 到 A,B 两点距离之和 PA+PB 的最小值为.如图,∠AOB=30°,点 M、N 分别是射线 OA、OB 上的动点,OP 平分∠AOB,且 OP=6,△PMN 的周长最小值为;当△PMN 的周长取最小值时,四边形 PMON 的面积为。变式:“造桥选址”模型如图,已知直线 a∥b,且 a 与 b 之间的距离为 4,点 A 到直线 a的距离为 2,点 B到直线 b 的距离为 3,AB= 2 30 .试在直线 a 上找一点 M,在直线 b 上找一点 N,满足 MN⊥a 且 AM+MN+NB 的长度和最短,则此时 AM+NB 的值为。如图,CD 是直线 y=x 上的一条定长的动线段,且 CD=2,点 A(4,0),连接AC、AD,设 C 点横坐标为 m,求 m 为何值时,△ACD 的周长最小,并求出这个值。二、“胡不归”模型有一则历史故事:说的是一个身在他乡的小伙子,得知父亲病危的消息后便日夜赶路回家。然而,当他气喘吁吁地来到父亲的面前时,老人刚刚咽气了。人们告诉他,在弥留之际,老人在不断喃喃地叨念:“胡不归?胡不归?”早期的科学家曾为这则古老的传说中的小伙子设想了一条路线。(如下图)A 是出发地,B 是目的地;AC 是一条驿道,而驿道靠目的地的一侧是沙地。为了急切回家,小伙子选择了直线路程 AB。但是,他忽略了在驿道上(V1)行走要比在砂土地带(V2)行走快的这一因素。如果他能选择一条合适的路线(尽管这条路线长一些,但速度可以加快),是可以提前抵达家门的。解题步骤:V2①将所求线段和改写为“BD+ V1V2AD”的形式(0...