中考必会几何模型：K型一线三垂直模型

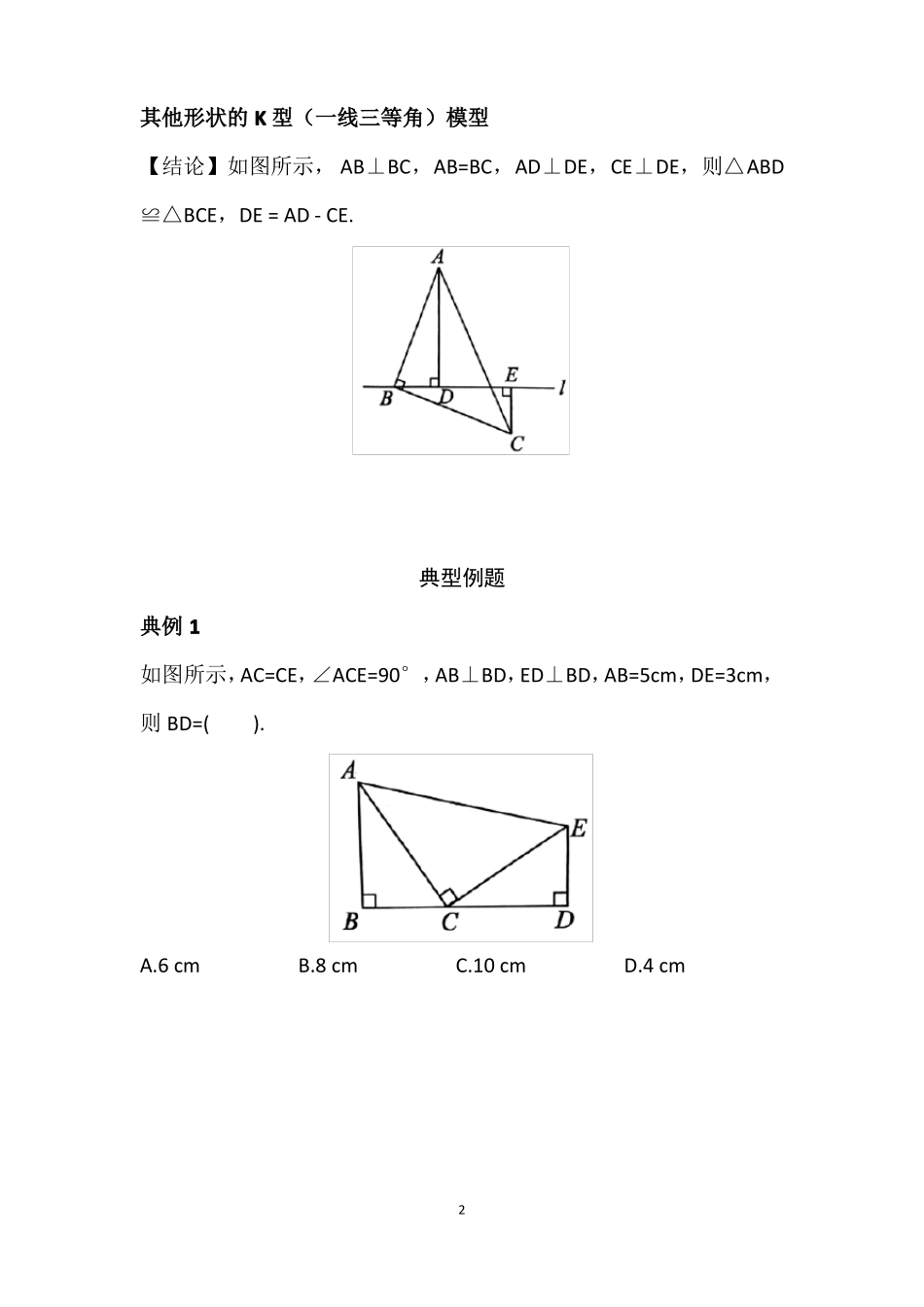
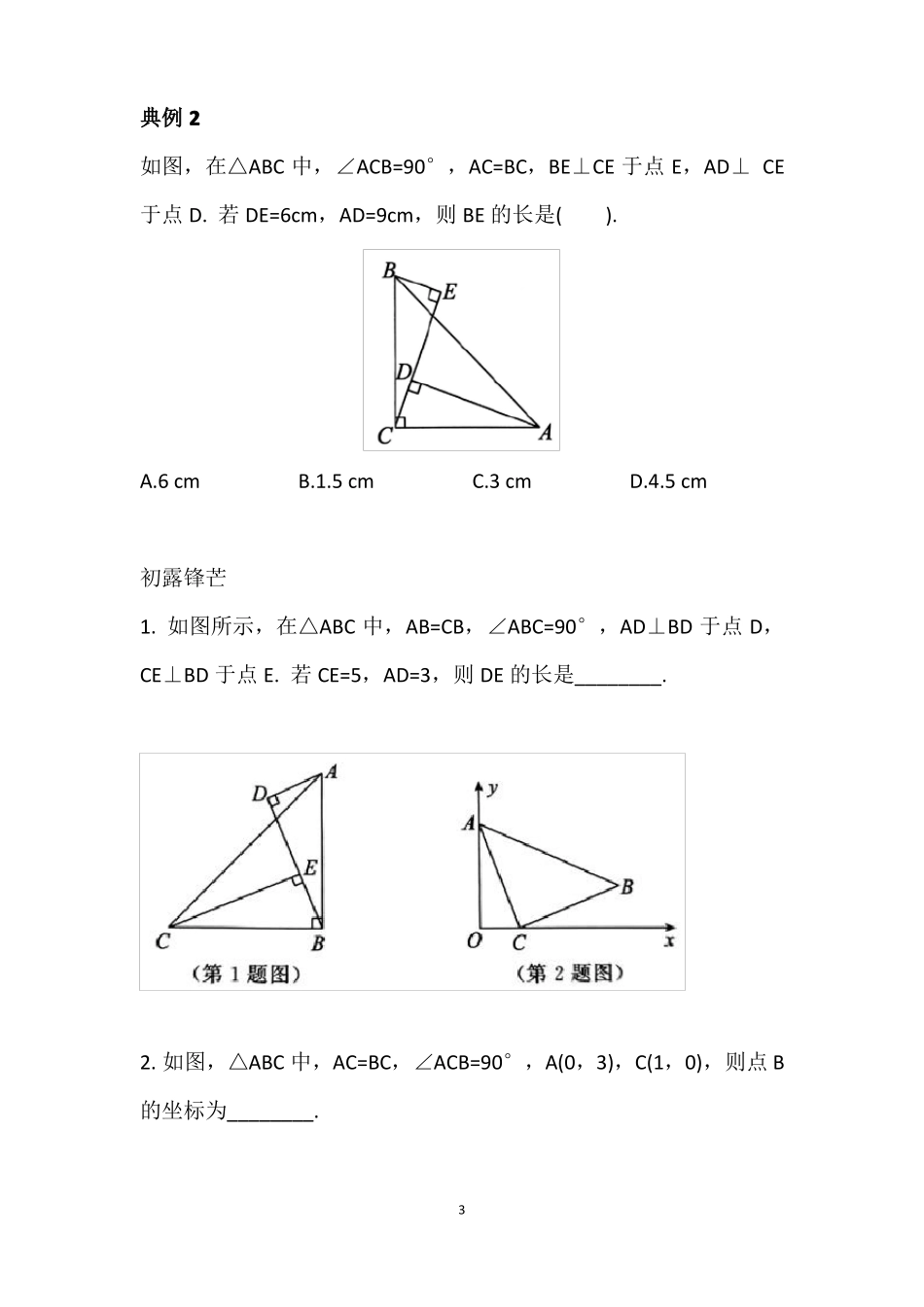
K 型（一线三垂直）模型讲解【结论】如图所示， AB⊥BC，AB=BC，AD⊥DE，CE⊥DE，则△ABD≌△BCE，DE=AD+CE.【证明】 AB⊥BC， ∴∠ABC=90°，∴∠ABD+∠EBC=90°. AD⊥DE，CE⊥DE，∴∠ADB=90°，∠BEC=90°,∴∠ABD+∠DAB = 90°，∠DAB=∠EBC.在△ABD 和△BCE 中，∠ADB = ∠BEC{∠DAB = ∠EBC∴△ABD≌△BCE(AAS)，∴AD=BE，DB=CE，∴DE=BE+DB=AD+CE.1AB = BC其他形状的 K 型（一线三等角）模型【结论】如图所示， AB⊥BC，AB=BC，AD⊥DE，CE⊥DE，则△ABD≌△BCE，DE = AD - CE.典型例题典例 1如图所示，AC=CE，∠ACE=90°，AB⊥BD，ED⊥BD，AB=5cm，DE=3cm，则 BD=().A.6 cmB.8 cmC.10 cmD.4 cm2典例 2如图，在△ABC 中，∠ACB=90°，AC=BC，BE⊥CE 于点 E，AD⊥ CE于点 D. 若 DE=6cm，AD=9cm，则 BE 的长是().A.6 cmB.1.5 cmC.3 cmD.4.5 cm初露锋芒1. 如图所示，在△ABC 中，AB=CB，∠ABC=90°，AD⊥BD 于点 D，CE⊥BD 于点 E. 若 CE=5，AD=3，则 DE 的长是________.2. 如图，△ABC 中，AC=BC，∠ACB=90°，A(0，3)，C(1，0)，则点 B的坐标为________.3感受中考1. (2018 山东临沂中考真题)如图，△ACB=90°，AC=BC，AD⊥CE，BE⊥CE，垂足分别是点 D，E，AD=3，BE=1，则 DE 的长是().A. 32B. 2C. 2√2D. √102. (2020 四川南充中考真题)如图，点 C 在线段 BD 上，且DE⊥BD，AC⊥CE，BC=DE.求证：AB=CD.4AB⊥BD，参考答案典型例题典例 1【答案】B【解析】易知本题为 K 型(一线三垂直)模型.根据 K 型(一线三垂直)模型的结论，可知两条手臂之间的距离＝长手＋短手，即 BD=AB+DE，∴BD=5+3=8(cm).故选 B.典例 2【答案】C【解析】易知本题为 K 型(一线三垂直)模型根据 K 型(一线三垂直)模型的结论，可知两条手臂之间的距离=长手 - 短手即 DE = AD - BE，∴BE=AD - DE= 9 - 6 = 3(cm).故选 C.5初露锋芒1.【答案】2【解析】由题图易知为 K 型(一线三垂直)模型，根据 K 型(一线三垂直)模型的结论，可知两条手臂之间的距离 = 长手 - 短手，即 DE = CE - AD = 5 - 3 = 2.2.【答案】(4，1)【解析】如图，作 BD⊥x 轴于点 D. BD⊥x 轴于点 D，由 K 型(一线三垂直)模型容易得△AOC≌△CDB，∴CD=AO，OC=BD. 点 C(1，0)，A(0，3)，∴OC=1，BD=1，CD=3.∴OD=4，∴点 B 的坐标为(4，1).6感受中考1.【答案】B【解析】由题...