人口增长模型

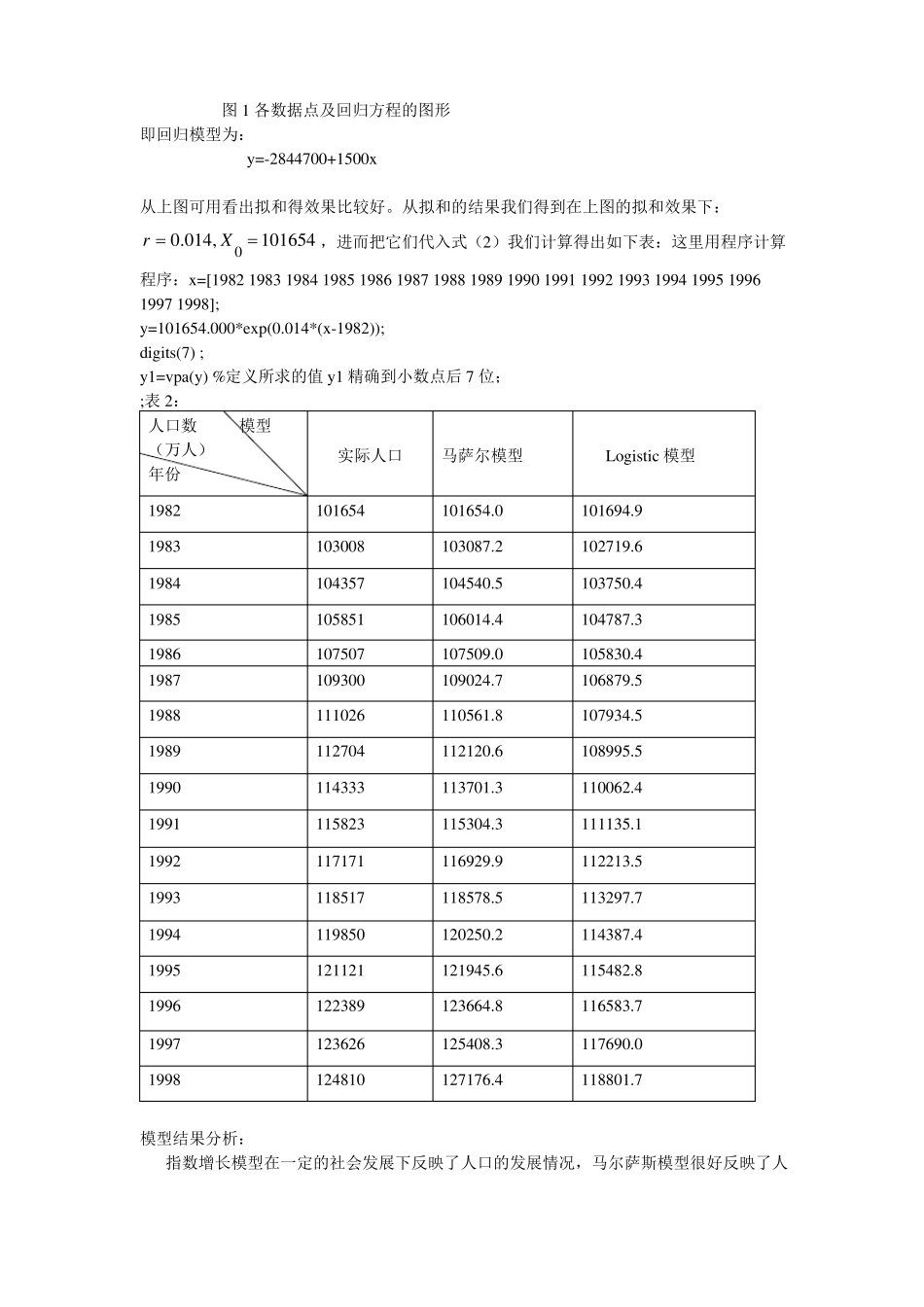
一、人口增长模型：1.问题下表列出了中国 1982—1998 年的人口统计数据，取 1982 年为起始年（t=0），…人口自然增长率 14%，以 36 亿作为我国的人口容纳量，是建立一个较好的数学模型并给出相应的算法和程序，并与实际人口相比较：时间（年） 1982人口（万人）时间人口时间人口1016541988111026199411985019831030081989112704199512112119841043571990114333199612238919851058511991115823199712362619861075071992117171199812481019871093001993118517从图中我们可以看到人口数在 1982—1998 年是呈增长趋势的，而且我们很容易发现上述图像和我们学过指数函数的图像有很大的相似性，所以我们很自然想到建立指数模型，但是指数模型有个不妥之处就是没有考虑社会因素的，即资源的有限性，也就是人口不可能无限制的增长，所以有必要改进模型，这里我们假设人口增长率随人口增加而呈线性递减，从而建立起比较优越阻滞增长模型模型一：指数增长模型（马尔萨斯模型）1.假设：人口增长率 r 是常数.2.建立模型：记时刻 t=0 时人口数为 X0 ,时刻 t 的人口为X（t）,由于量大，X（t）可以视为连续、可微函数，t 到 t+t 时间段人口的增量为：X (t  t)  X (t)  rX (t)tdx rX于是 X（t）满足微分方程：dt(1)X (0)  X 03.模型求解：解得微分方程（1）得：X（t）= X 0 er(tt0)（2）(r.  0) . 时， Xt 表明：t 4.模型的参数估计要用模型 2 对人口进行预报，必须对其中的参数 r 进行估计，这可以用表 1 通过 Matlab拟合：程序：x=[1982 1983 1984 1985 1986 1987 1988 1989 1990 1991 1992 1993 1994 1995 1996 19971998]';X=[ones(17,1),x]Y=[101654 103008 104357 105851 107507 109300 111026 112704 114333 115823 117171118517 119850 121121 122389 123626 124810]';[b,bint,r,rint,stats]=regress(Y,X); %回归分析b,bint,stats%输出这些值rcoplot(r,rint);%画出残差及其置信区间z=b(1)+b(2)*x;plot(x,Y,'k+',x,z,'r')，%预测及作图运行结果：b =1.0e+006 *-2.84470.0015bint =1.0e+006 *-2.9381-2.75130.00140.0015stats =1.0e+005 *0.00000.045501.9800图 1 各数据点及回归方程的图形即回归模型为：y=-2844700+1500x从上图可用看出拟和得效果比较好。从拟和的结果我们得到在上图的拟和效果下：r...