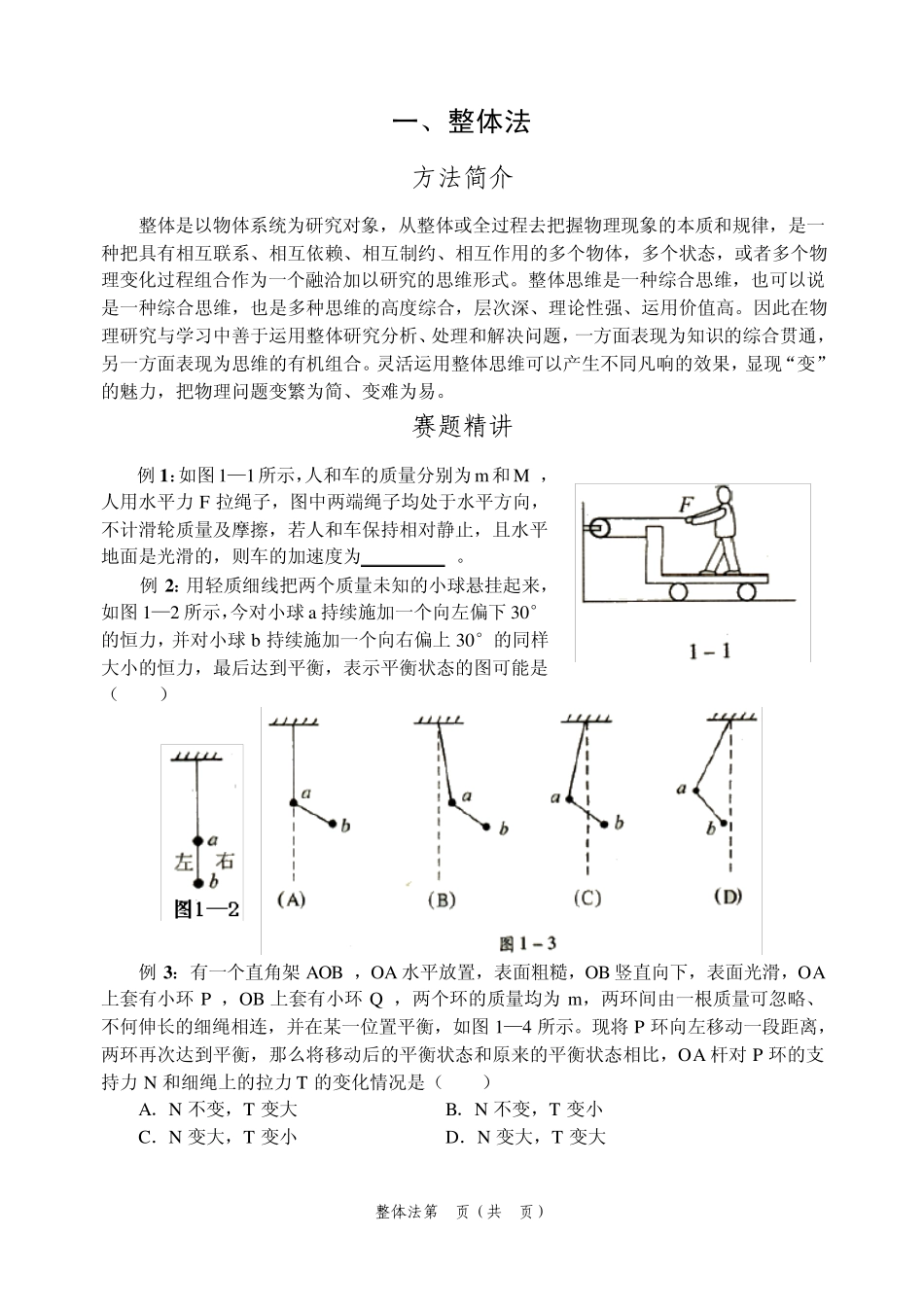
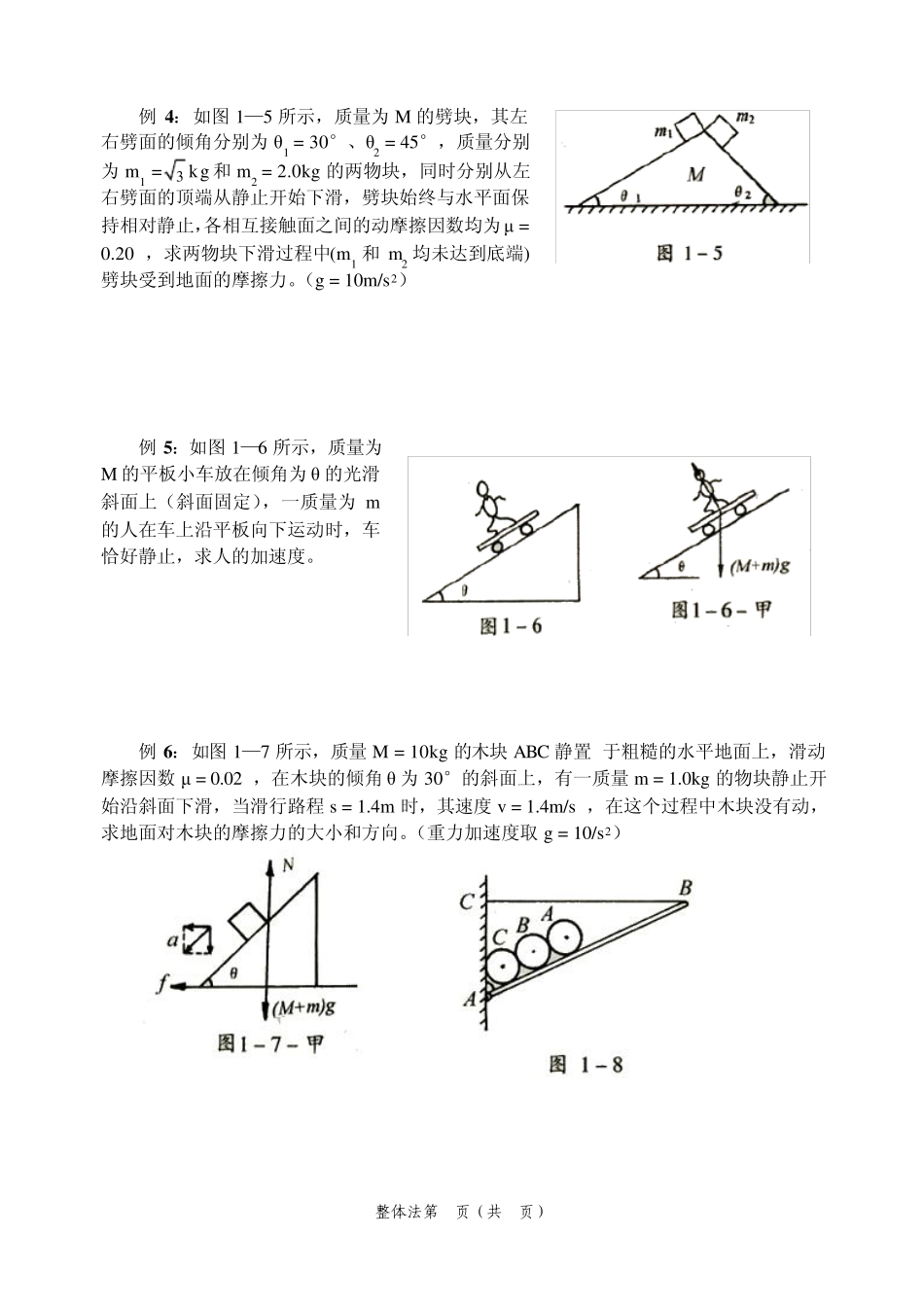
整体法第1页(共9页) 一、整体法 方法简介 整体是以物体系统为研究对象,从整体或全过程去把握物理现象的本质和规律,是一种把具有相互联系、相互依赖、相互制约、相互作用的多个物体,多个状态,或者多个物理变化过程组合作为一个融洽加以研究的思维形式。整体思维是一种综合思维,也可以说是一种综合思维,也是多种思维的高度综合,层次深、理论性强、运用价值高。因此在物理研究与学习中善于运用整体研究分析、处理和解决问题,一方面表现为知识的综合贯通,另一方面表现为思维的有机组合。灵活运用整体思维可以产生不同凡响的效果,显现“变”的魅力,把物理问题变繁为简、变难为易。 赛题精讲 例 1:如图1—1所示,人和车的质量分别为m 和M ,人用水平力 F 拉绳子,图中两端绳子均处于水平方向,不计滑轮质量及摩擦,若人和车保持相对静止,且水平地面是光滑的,则车的加速度为 。 例 2:用轻质细线把两个质量未知的小球悬挂起来,如图 1—2 所示,今对小球a 持续施加一个向左偏下30°的恒力,并对小球b 持续施加一个向右偏上 30°的同样大小的恒力,最后达到平衡,表示平衡状态的图可能是( ) 例 3:有一个直角架 AOB ,OA 水平放置,表面粗糙,OB 竖直向下,表面光滑,OA上套有小环 P ,OB 上套有小环 Q ,两个环的质量均为 m ,两环间由一根质量可忽略、不何伸长的细绳相连,并在某一位置平衡,如图 1—4 所示。现将 P 环向左移动一段距离,两环再次达到平衡,那么将移动后的平衡状态和原来的平衡状态相比,OA 杆对 P 环的支持力 N 和细绳上的拉力 T 的变化情况是( ) A.N 不变,T 变大 B.N 不变,T 变小 C.N 变大,T 变小 D.N 变大,T 变大 整体法第 2页(共 9页) 例4:如图1—5 所示,质量为M 的劈块,其左右劈面的倾角分别为θ1 = 30°、θ2 = 45°,质量分别为m1 =3 kg 和 m2 = 2.0kg 的两物块,同时分别从左右劈面的顶端从静止开始下滑,劈块始终与水平面保持相对静止,各相互接触面之间的动摩擦因数均为μ = 0.20 ,求两物块下滑过程中(m1 和 m2 均未达到底端)劈块受到地面的摩擦力。(g = 10m/s2) 例5:如图1—6 所示,质量为M 的平板小车放在倾角为θ 的光滑斜面上(斜面固定),一质量为m的人在车上沿平板向下运动时,车恰好静止,求人的加速度。 例6:如图1—7 所示,质量M = 10kg 的木块ABC 静置 于粗糙的水平地面上,...