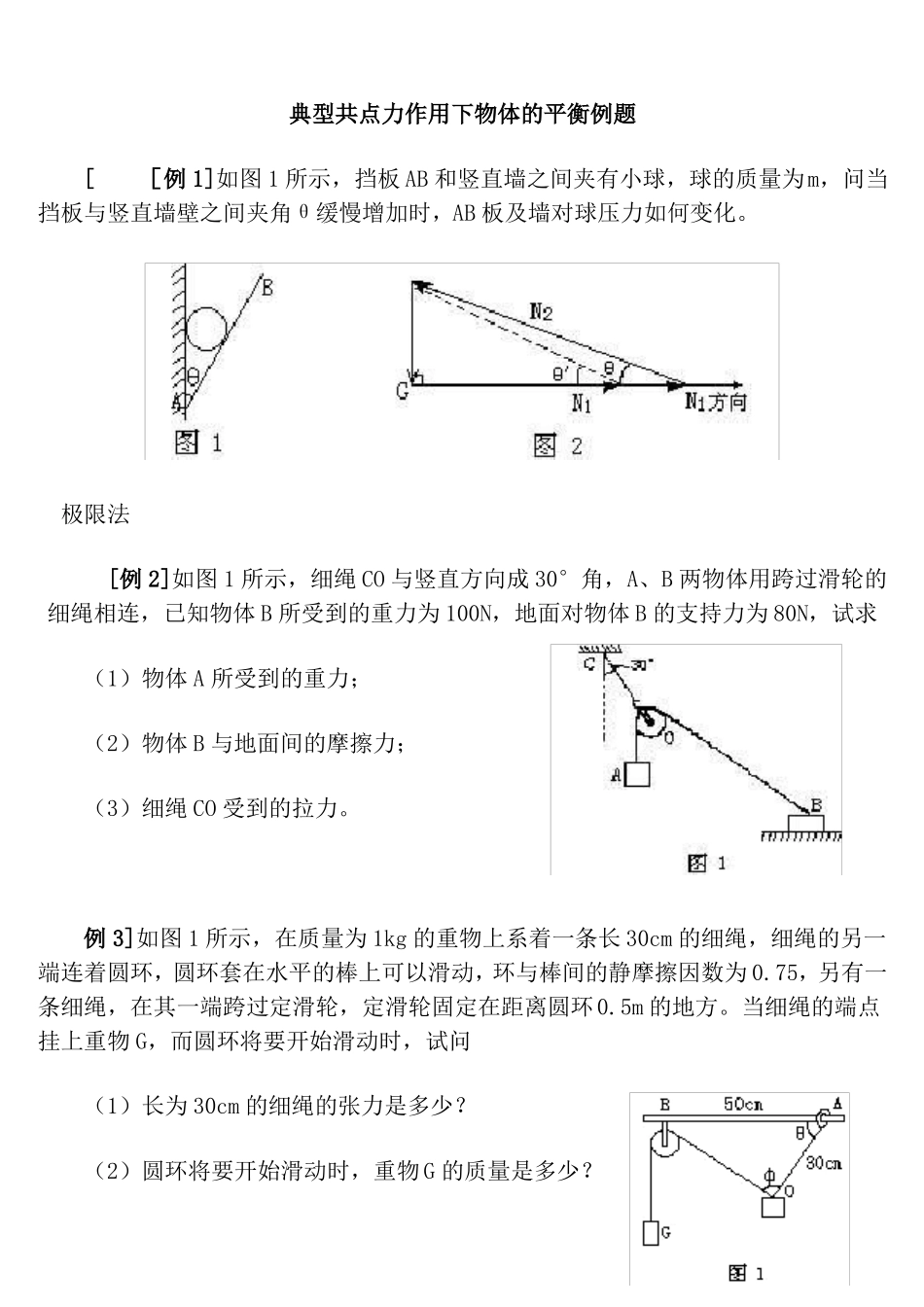
典型共点力作用下物体的平衡例题[[例 1]如图 1 所示,挡板 AB 和竖直墙之间夹有小球,球的质量为m,问当挡板与竖直墙壁之间夹角θ缓慢增加时,AB 板及墙对球压力如何变化。极限法[例 2]如图 1 所示,细绳 CO 与竖直方向成 30°角,A、B 两物体用跨过滑轮的细绳相连,已知物体 B 所受到的重力为 100N,地面对物体 B 的支持力为 80N,试求(1)物体 A 所受到的重力;(2)物体 B 与地面间的摩擦力;(3)细绳 CO 受到的拉力。例 3]如图 1 所示,在质量为 1kg 的重物上系着一条长 30cm 的细绳,细绳的另一端连着圆环,圆环套在水平的棒上可以滑动,环与棒间的静摩擦因数为 0.75,另有一条细绳,在其一端跨过定滑轮,定滑轮固定在距离圆环0.5m 的地方。当细绳的端点挂上重物 G,而圆环将要开始滑动时,试问(1)长为 30cm 的细绳的张力是多少?(2)圆环将要开始滑动时,重物 G 的质量是多少?(3)角φ多大?[分析]选取圆环作为研究对象,分析圆环的受力情况:圆环受到重力、细绳的张力 T、杆对圆环的支持力 N、摩擦力 f 的作用。[解]因为圆环将要开始滑动,所以,可以判定本题是在共点力作用下物体的平衡问题。由牛顿第二定律给出的平衡条件∑Fx=0,∑Fy=0,建立方程有μN-Tcosθ=0,N-Tsinθ=0。设想:过 O 作 OA 的垂线与杆交于 B′点,由 AO=30cm,tgθ=, 得 B′O 的长为 40cm。在直角三角形中,由三角形的边长条件得 AB′=50cm,但据题述条件 AB=50cm,故 B′点与滑轮的固定处 B 点重合,即得φ=90°。(1)如图 2 所示选取坐标轴,根据平衡条件有Gcosθ+Tsinθ-mg=0,Tcosθ-Gsinθ=0。解得 T≈8N,(2)圆环将要滑动时,得 mGg=Tctgθ, mG=0.6kg。(3)前已证明φ为直角。例 4]如图 1 所示,质量为 m=5kg 的物体放在水平面上,物体与水平面间的动摩擦因数求当物体做匀速直线运动时,牵引力 F 的最小值和方向角θ。[分析]本题考察物体受力分析:由于求摩擦力 f 时,N 受 F 制约,而求 F 最小值,即转化为在物理问题中应用数学方法解决的实际问题。我们可以先通过物体受力分析。据平衡条件,找出 F 与θ关系。进一步应用数学知识求解极值。[解] 作出物体 m 受力分析如图 2,由平衡条件。∑Fx=Fcosθ-μN=0 (1)∑Fy=Fsinθ+N-G=0 (2)由 cos(θ-Ф)=1 即 θ—Ф=0 时∴ Ф=30°,θ=30°[说明] 本题中我们应用了数学上极值方法,来求解物...