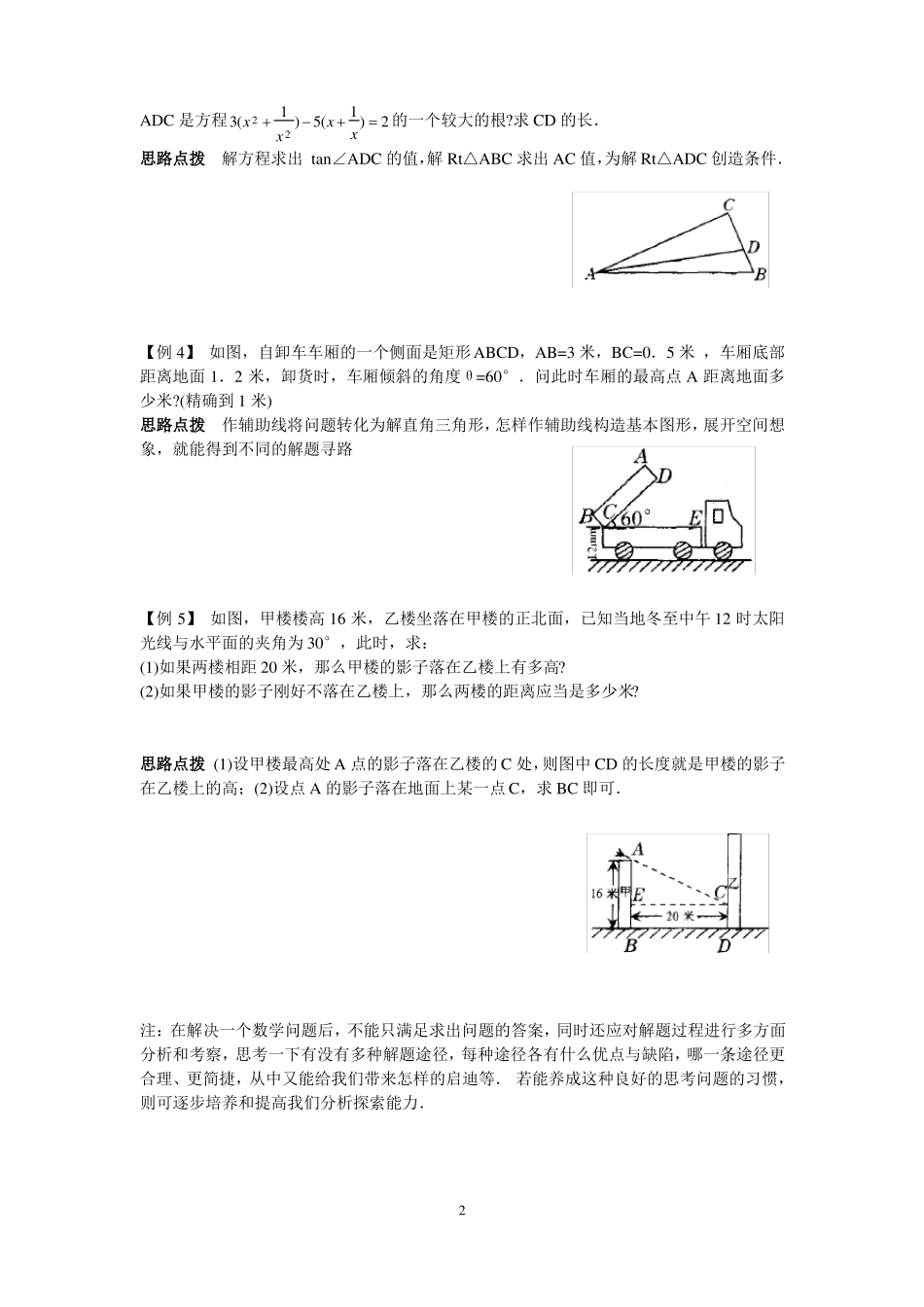
初中数学竞赛辅导讲义---解直角三角形利用直角三角形中的已知元素 (至少有一条是边)求得其余元素的过程叫做解直角三角形,解直角三角形有以下两方面的应用:1.为线段、角的计算提供新的途径.解直角三角形的基础是三角函数的概念,三角函数使直角三角形的边与角得以转化,突破纯粹几何关系的局限.2.解实际问题.测量、航行、工程技术等生活生产的实际问题,许多问题可转化为解直角三角形获解,解决问题的关键是在理解有关名词的意义的基础上,准确把实际问题抽象为几何图形,进而转化为解直角三角形.【例题求解】【例 1】 如图,已知电线杆 AB 直立于地面上,它的影子恰好照在土坡的坡面 CD 和地面BC 上,如果CD 与地面成 45°,∠A=60°,CD=4m,BC=( 4 6 2 2 )m,则电线杆AB的长为.思路点拨延长 AD 交 BC 于 E,作 DF⊥BC 于 F,为解直角三角形创造条件.【例 2】如图,在四边形 ABCD 中,AB= 4 2 ,BC-1,CD=3 ,∠B=135°,∠C=90°,则∠D 等于()A.60°B.67.5°C.75°D.无法确定思路点拨通过对内分割或向外补形,构造直角三角形.注:因直角三角形元素之间有很多关系,故用已知元素与未知元素的途径常不惟一,选择怎样的途径最有效、最合理呢?请记住:有斜用弦,无斜用切,宁乘勿除.在没有直角的条件下,常通过作垂线构造直角三角形;在解由多个直角三角形组合而成的问题时,往往先解已具备条件的直角三角形,使得求解的直角三角形最终可解.【例 3】如图,在△ABC 中,∠=90°,∠BAC=30°,BC=l,D 为 BC 边上一点,tan∠1ADC 是方程3(x 2 1) 5(x ) 2 的一个较大的根?求 CD 的长.2xx1思路点拨解方程求出 tan∠ADC 的值,解 Rt△ABC 求出 AC 值,为解 Rt△ADC 创造条件.【例 4】 如图,自卸车车厢的一个侧面是矩形 ABCD,AB=3 米,BC=0.5 米 ,车厢底部距离地面 1.2 米,卸货时,车厢倾斜的角度θ=60°.问此时车厢的最高点 A 距离地面多少米?(精确到 1 米)思路点拨作辅助线将问题转化为解直角三角形,怎样作辅助线构造基本图形,展开空间想象,就能得到不同的解题寻路【例 5】 如图,甲楼楼高 16 米,乙楼坐落在甲楼的正北面,已知当地冬至中午 12 时太阳光线与水平面的夹角为 30°,此时,求:(1)如果两楼相距 20 米,那么甲楼的影子落在乙楼上有多高?(2)如果甲楼的影子刚好不落在乙楼上,那么两楼的距离应当是多少米?思...