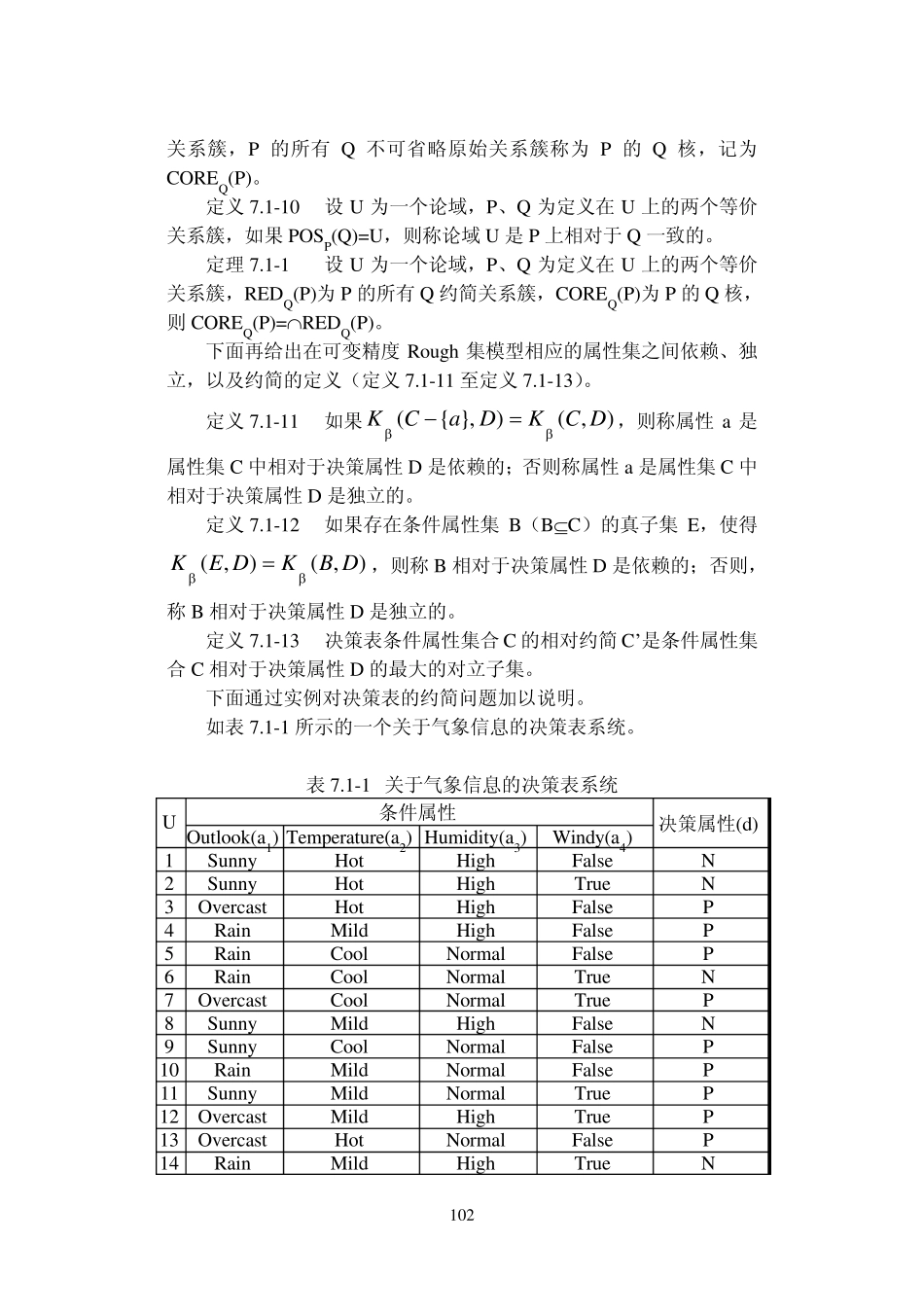
100 第七章 信息表属性约简 基于 Rough 集理论的知识获取,主要是通过对原始决策表的约简,在保持决策表决策属性和条件属性之间的依赖关系不发生变化的前提下对决策表进行约简(简化),包括属性约简和值约简。本章将对决策表的属性约简从代数集合观点和信息论的信息熵观点进行系统分析,并介绍几种有效的属性约简算法。 7 .1 决策表属性约简概述 一个决策表就是一个决策信息系统,表中包含了大量领域样本(实例)的信息。在第四章中,我们曾经对决策规则进行了讨论,决策表中的一个样本就代表一条基本决策规则,如果我们把所有这样的决策规则罗列出来,就可以得到一个决策规则集合,但是,这样的决策规则集合是没有什么用处的,因为其中的基本决策规则没有适应性,只是机械地记录了一个样本的情况,不能适应新的、其他的情况。为了从决策表中抽取得到适应度大的规则,我们需要对决策表进行约简,使得经过约简处理的决策表中的一个记录就代表一类具有相同规律特性的样本,这样得到的决策规则就具有较高的适应性。 根据定义 2.1-1,我们可以进一步讨论决策表中属性的必要性和相应的约简算法。 定义 7.1-1 设 U 是一个论域,P 是定义在 U 上的一个等价关系簇,RP。如果 IND(P-{R})=IND(P),则称关系 R 在 P 中是绝对不必要的(多余的);否则,称 R 在 P 中是绝对必要的。 绝对不必要的关系在知识库中是多余的,如果将它们从知识库中去掉,不会改变该知识库的分类能力。相反,若知识库中去掉一个绝对必要的关系,则一定改变知识库的分类能力。 定义 7.1-2 设 U 为一个论域,P 为定义在 U 上的一个等价关系簇,RP。如果每个关系 RP 在 P 中都是绝对必要的,则称关系簇 P是独立的;否则,称 P 是相互依赖的。 对于相互依赖的关系簇来说,其中包含有冗余关系,可以对其约简;而对于独立的关系簇,去掉其中任何一个关系都将破坏知识库的分类能力。 101 定义7.1-3 设U 为一个论域,P 为定义在U 上的一个等价关系簇,P 中所有绝对必要关系组成的集合,称为关系簇P 的绝对核,记作CORE(P)。 定义7.1-4 设U 为一个论域,P、Q 为定义在U 上的两个等价关系簇,且 QP。 如果 (1) IND(Q)=IND(P); (2) Q 是独立的; 则称Q 是 P 的一个绝对约简。 如果知识 Q 是知识 P 的绝对约简,那么,U 中通过知识 P 可区分的对象,同样可以用知识 Q 来区分。 在讨论决策表信息系统...