单纯形法习题详解-单纯形法练习题

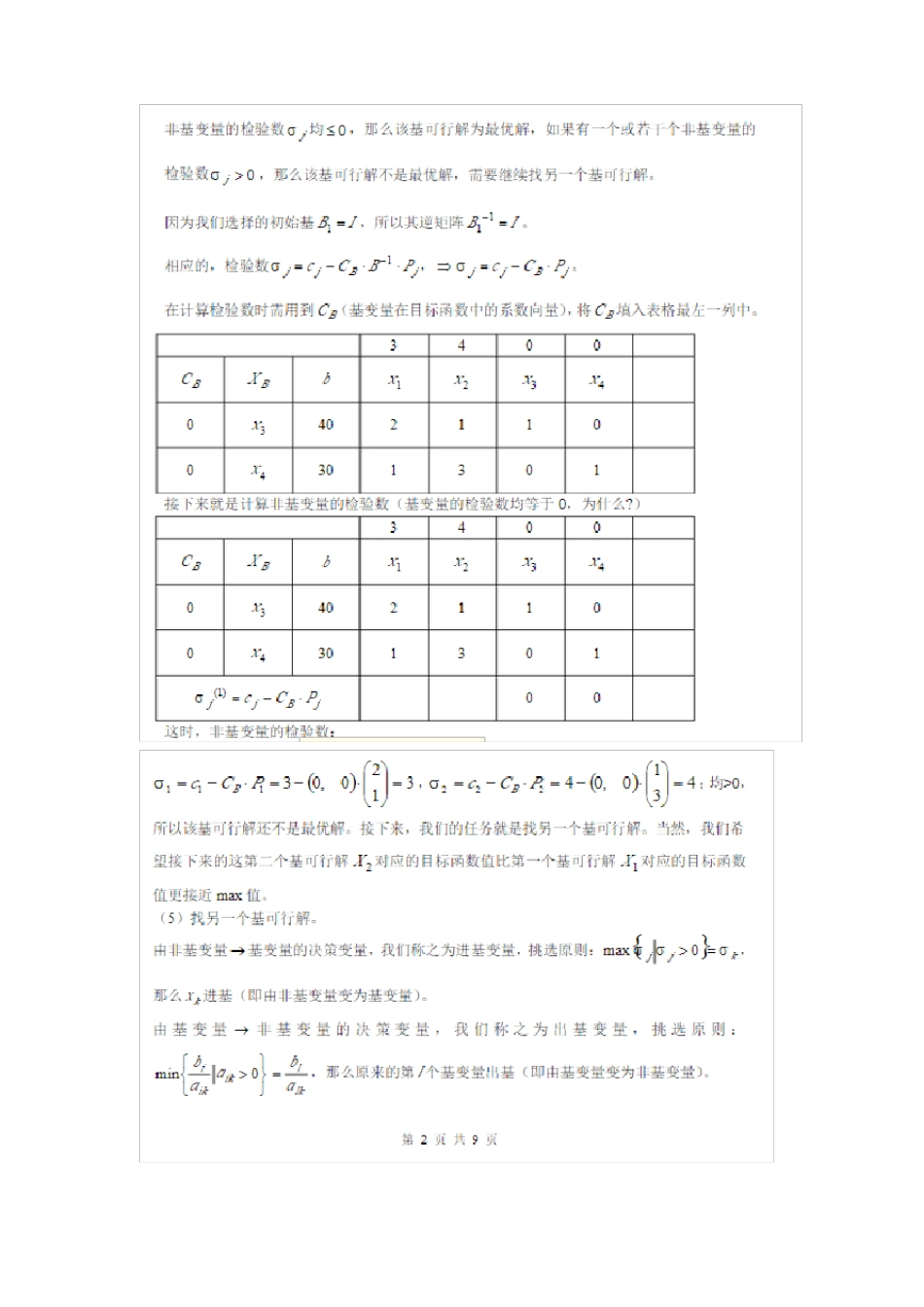
单纯形法应用实例某工厂生产 I，II 两种商品，已知生产单位商品所需要的设备台时，A、B 两种原材料的消耗、设备使用台时限额以及原材料的限额如下表所示。该工厂生产一件商品 I 可获利 3 元，每生产一件商品 II 可获利 4 元。写出使该工厂所获利润最大的线性规划模型，并用单纯型法求解。产品 I产品 II限额设备原材料211340 台时30KG用单纯形法求解该线性规划问题max z  2x1  x25x2 156x  2x  2412s..t x  x  512x ,x  012cjb152452x11x20x30x40x5无穷CB基x3000cj  zj05211100001000010x4x561245（检验数）首先列出表格，先确定正检验数最大值所在列为主列，然后用b 除以主列上对应的同行数字。除出来所得值最小的那一行为主行，根据主行和主列可以确定主元（交点）。接着把主元化为 1并把 X4 换成 X1.cjb15452x11x20x30x40x5CB基x3020011252/611100001/6000010x1x5cj  zj这时进行初等行列变换，把主列换单位向量，主元为 1。也就是 X5 所在行减去 X1 所在行。并且重新计算检验数。cj21000CB基x3b1545-4x1x2x3x4x50200152/6100001/60-1/6=-1/60-0*0-2*1/6-0*-1/6=-1/30010x1x51-1=01-2/6=4/62-2*1-0*0-0*1=01-0*5-2*2/6-0*4/6=1/3cj  zj再次确定主元。为 4/6。然后把 X5 换成 X2。并且把主元化成 1。cjb1546/42x11x20x30x40x5CB基x3020010052/611100001/6-1/4-1/3006/40x1x2cj  zj然后再用 X1 行减去 2/6 倍的 X2 行，X3 行减去 5 倍的 X2 行。并且重新计算检验数。cjb15/27/23/22x11x20x30x40x5CB基x30210100011005/41/4-1/4-15/2-1/23/2x1x2cjzj000-1/4-1/2最后得到的表格中检验数这一行无正数则所得解为最优解。本题最优解为 X=(7/2,3/2,15/2,0,0)目标函数值 Z=8.5