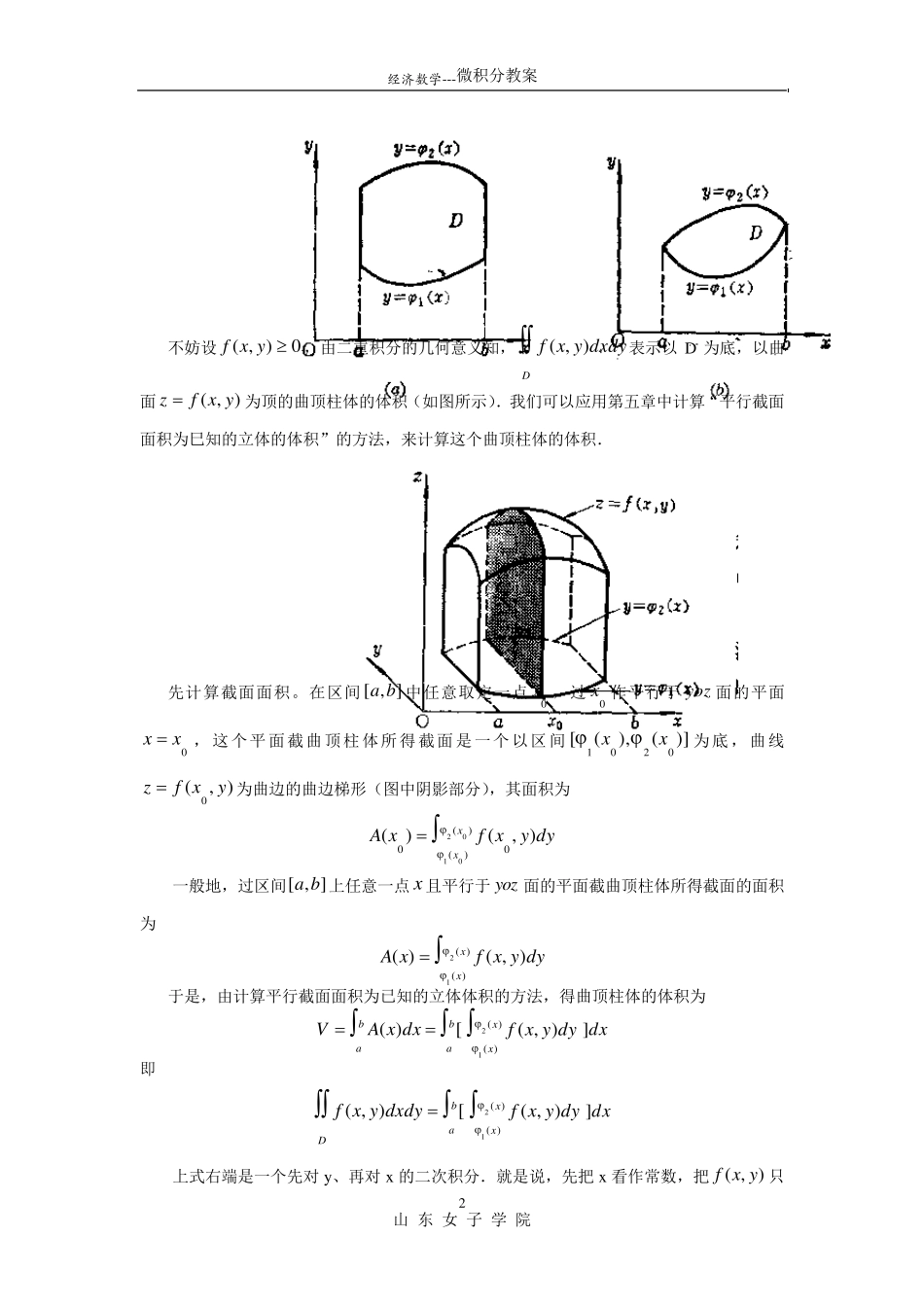
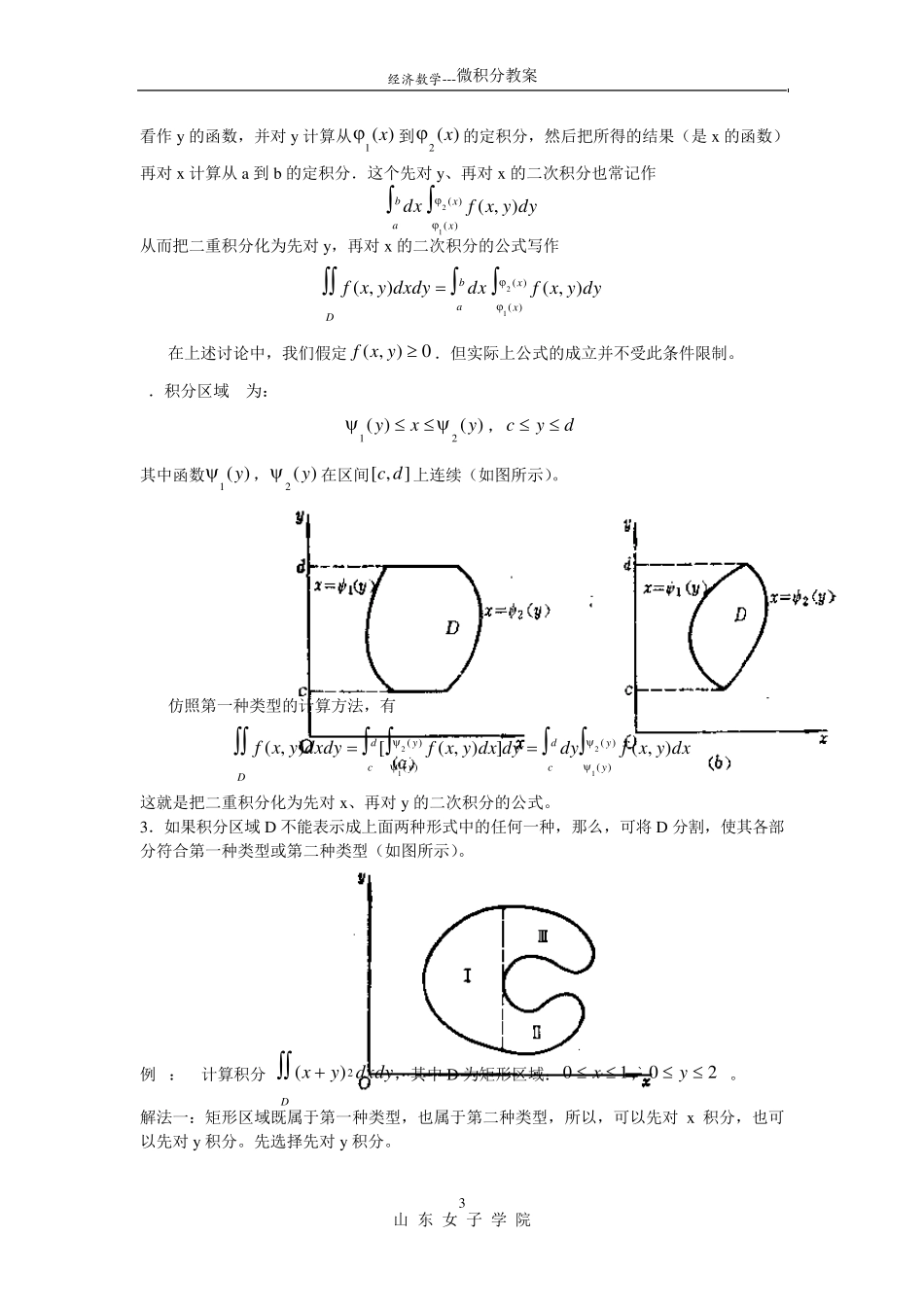
经济数学---微积分教案 山 东 女 子 学 院 1 第二节 二重积分的计算 教学目的:掌握二重积分的计算方法,能正确计算二重积分 教学重点: 二重积分计算 教学难点: 利用极坐标计算二重积分、应用 教学时数:6 教学内容: 一般情况下,直接利用二重积分的定义计算二重积分是非常困难的,二重积分的计算可以归结为求二次定积分(即二次积分)。现在我们由二重积分的几何意义导出二重积分的计算方法。 一、利用直角坐标系计算二重积分 若二重积分存在,和式极限值与区域 D 的分法无关,故在直角坐标系下我们用与坐标轴平行的两组直线把 D 划分成各边平行于坐标轴的一些小矩形(如图所示),于是小矩形的面积yx ,因此在直角坐标系下,面积元素为: dx dyd 于是二重积分可写成 Ddyxf),(Ddx dyyxf),( 现在,我们根据二重积分的几何意义,结合积分区域的几种形状,推导二重积分的计算方法。 1.积分区域 D 为: bxa,)()(21xyx 其中函数)(1 x,)(2 x在],[ ba上连续(如图所示)。 经济数学---微积分教案 山 东 女 子 学 院 2 不妨设0),(yxf,由二重积分的几何意义知,Ddxdyyxf),(表示以D 为底,以曲面),(yxfz 为顶的曲顶柱体的体积(如图所示).我们可以应用第五章中计算“平行截面面积为巳知的立体的体积”的方法,来计算这个曲顶柱体的体积. 先计算截面面积。在区间],[ba中任意取定一点0x ,过0x 作平行于 yoz 面的平面0xx ,这个平面截曲顶柱体所得截面是一个以区间)](),([0201xx为底,曲线),(0 yxfz 为曲边的曲边梯形(图中阴影部分),其面积为 )()(000201),()(xxdyyxfxA 一般地,过区间],[ba上任意一点 x 且平行于 yoz 面的平面截曲顶柱体所得截面的面积为 )()(21),()(xxdyyxfxA 于是,由计算平行截面面积为已知的立体体积的方法,得曲顶柱体的体积为 babadxxAV[)()()(21),(xxdyyxfdx] 即 Ddxdyyxf),(ba[ )()(21),(xxdyyxfdx] 上式右端是一个先对 y、再对 x 的二次积分.就是说,先把 x 看作常数,把),(yxf只经济数学---微积分教案 山 东 女 子 学 院 3 看作y 的函数,并对y 计算从)(1 x到)(2 x的定积分,然后把所得的结果(是x 的函数)再对x 计算从a 到b 的定积分.这个先对y、再对x 的二次积分也常记作 badx )()(21),(xxdyyx...