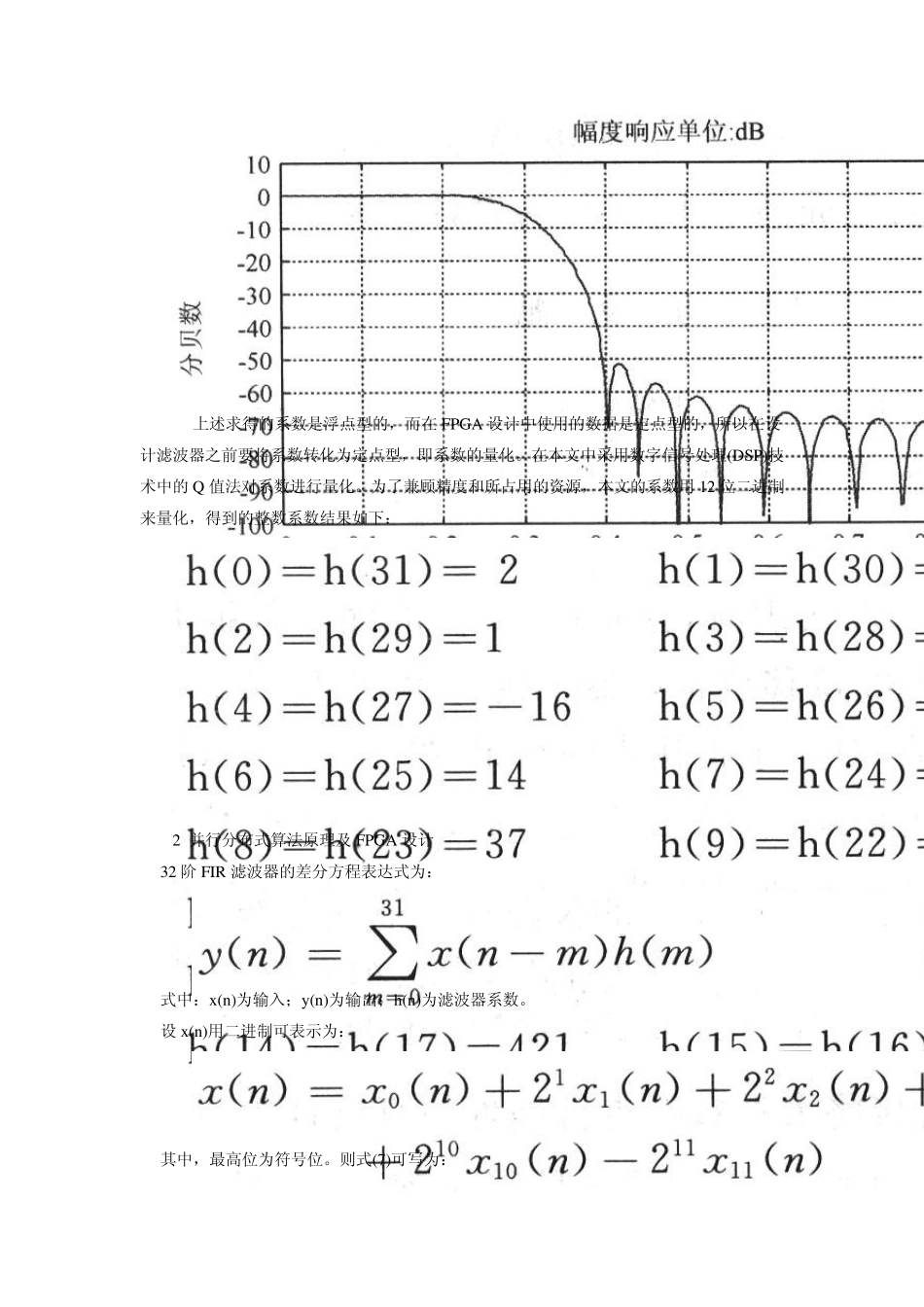
32 阶 FIR 滤波器的 FPGA 实现 随着软件无线电的发展。对于滤波器的处理速度要求越来越高。传统的 FIR 滤波器一般采用通用 DSP 处理器,但是 DSP 处理器采用的是串行运算,而 FPGA 是现场可编程阵列,可以实现专用集成电路,另外还可以采用纯并行结构及考虑流水线结构,因此在处理速度上可以明显高于 DSP 处理器。本文采用并行分布式算法在 FPGA 上设计并实现了高速处理的32 阶 FIR 低通滤波器,在此过程中利用 Matlab 的数值计算与分析功能来提高设计效率。 1 FlR 低通滤波器的窗函数实现 理想的滤波器频率响应中傅里叶反变换 ha(n)一定是无限长的序列,而且是非因果的,而实际要设计的滤波器 h(n)是有限长的,因此要用有限长来逼近无限长的,其方法就是用一个有限长度的窗口函数序列 ω(n)来截取,即: 常见的窗函数有矩形窗、巴特利特窗、汉宁窗、哈明窗、布莱克曼窗、凯泽窗。其中,凯泽窗提供了可变的过渡带宽。本文采用凯泽窗对 FIR 滤波器进行设计,其窗函数表达式为: I0[?]为第一类变形零阶贝赛尔函数,形状参数 β为依赖于滤波器阶数 M 的参数,用来调整主瓣宽度与旁瓣衰减,选择 M 可产生各种过渡带宽和接近最优的阻带衰减。给定通带截止频率 ωp,阻带起始频率 ωs,阻带衰减 As,凯泽窗设计中有经典公式可供使用,如下: 过渡带宽: 滤波器阶数: 假设低通数字滤波器设计指标如下: 采用上面介绍的凯泽窗,利用 Matlab 编程计算得到 32 阶 FIR 低通滤波器参数如下: 32 阶FIR 低通滤波器幅频特性图如图1 所示。 上述求得的系数是浮点型的,而在FPGA 设计中使用的数据是定点型的,所以在设计滤波器之前要将系数转化为定点型,即系数的量化。在本文中采用数字信号处理(DSP)技术中的Q 值法对系数进行量化。为了兼顾精度和所占用的资源,本文的系数用12 位二进制来量化,得到的整数系数结果如下: 2 并行分布式算法原理及 FPGA 设计 32 阶 FIR 滤波器的差分方程表达式为: 式中:x(n)为输入;y(n)为输出;h(n)为滤波器系数。 设x(n)用二进制可表示为: 其中,最高位为符号位。则式(7)可写为: 式(10)为并行分布式算法,由上可以看出并行分布式算法是将滤波器表达式重新排列,分别加权求和。与传统算法最大的不同之处是在 FPGA 设计过程中以查找表代替乘法器,即根据输入数据的不同,将对应的滤波器系数预先求和保存在 ROM 中,也就是将每一项的乘法求和通过...