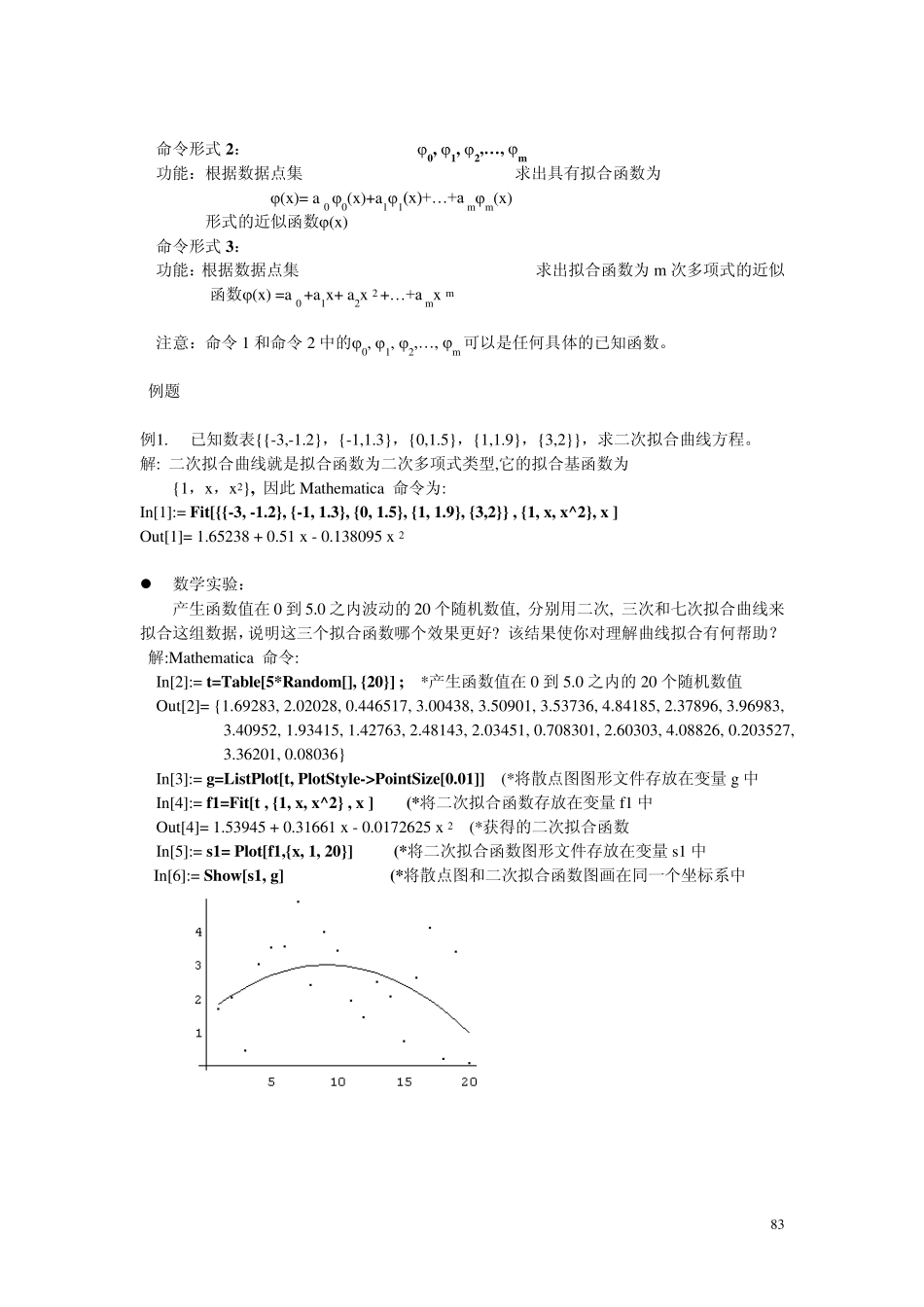
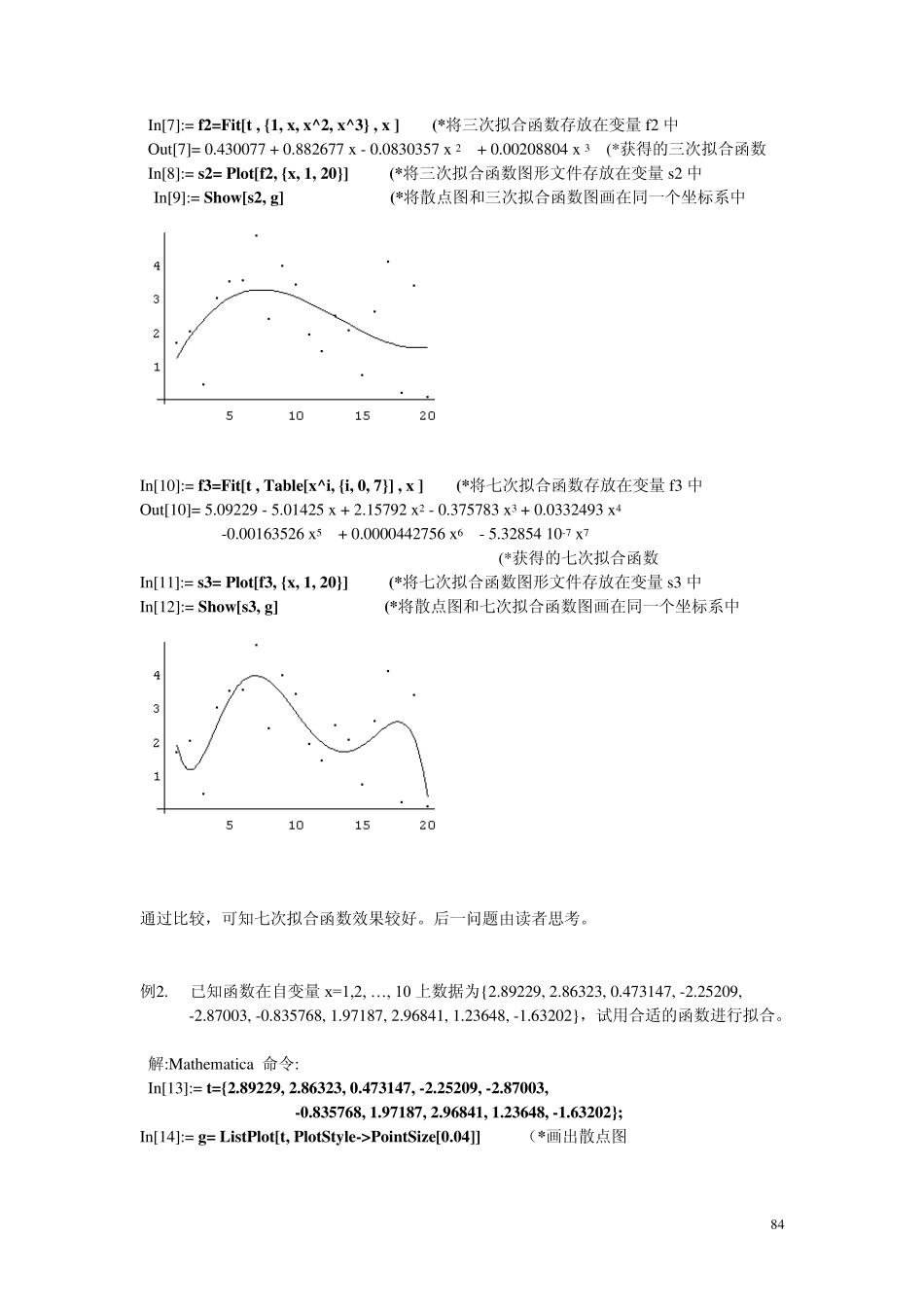
82 第六章 数值计算命令与例题 数值问题由一组已知数据来求出一组结果数据,使得这两组数据之间满足预先制定的某种关系的问题,数值计算就是通过对数学问题解有效的近似处理去获得比较满意解的计算方法。这里只介绍与数值计算中最基本方法的一些命令与例题。 6.1 求近似函数 在生产和实验中, 人们经常遇到需要通过某个未知(或复杂)的函数f(x )在有限个给定点的函数值:{xi, yi}, i=1,2,… ., n, 这里 f(x i) = y i 去获得函数f(x )的近似函数(x), 以便于处理涉及到f(x)的计算或其他处理问题, 这种求近似函数(x)的方法主要有拟合方法和插值方法。 一般, 曲线拟合是常用的拟合方法, 而插值方法常用的有多项式插值与分段插值方法, 在Mathematica 中它们都有相应的命令来获得相应的近似函数。 6.1.1 曲线拟合 曲线拟合主要用来求一元近似函数, 它是根据一组函数值(通常是测量值或试验数据)去寻找描述相应函数关系的一种常用数据逼近方法, 是根据最小二乘原理的意义下获得近似函数的, 此近似函数具有在数据点处的误差平方和最小的特点。通过拟合得到的函数关系通常称为经验公式, 该函数不必经过任何的数据点, 是实际函数的一种近似函数。曲线拟合结果的好坏与选用什么类型的函数作为拟和曲线类型有关。记函数集合: M=Span[0, 1, 2,… , m]={ (x)| (x)= a 0 0(x)+a11(x)+… +a mm(x), a i R} 称集合 M 为函数0, 1, 2,… , m 张成的空间,m+1 个函数0(x), 1(x), 2(x),… , m(x)称为拟合基函数集合, 它们都是已知的函数。拟合基函数集合不同对应不同的拟合函数类, 如果要用曲线拟合方法得到经验公式, 通常是先画出所给数据的散点图, 再根据散点图选择合适的拟和函数类型做曲线拟合。应该注意的是:选择不同的拟合函数类会得到不同的拟合函数,拟合函数的好坏依赖于所选的拟合函数类,如果你知道的曲线类型多, 就容易获得满意的拟合函数。利用 Mathematica 提供的曲线拟合命令可以方便快速地尝试各种不同的拟合函数类型可以帮你找到满意的近似函数。 Mathematica 曲线拟合的一般形式为: Fit[{数据点集合} , {拟合基函数集合} , 自变量名] 具体的拟合命令有: 命令形式 1:Fit[{{x1,y1},{x2,y2},...,{xn,yn}},{ 0, 1, 2,… , m },x] 功能:根据数据点集{{x1,y1},{x2,y2},...,{xn,yn}}求出具有拟合函数为 (x )= a ...