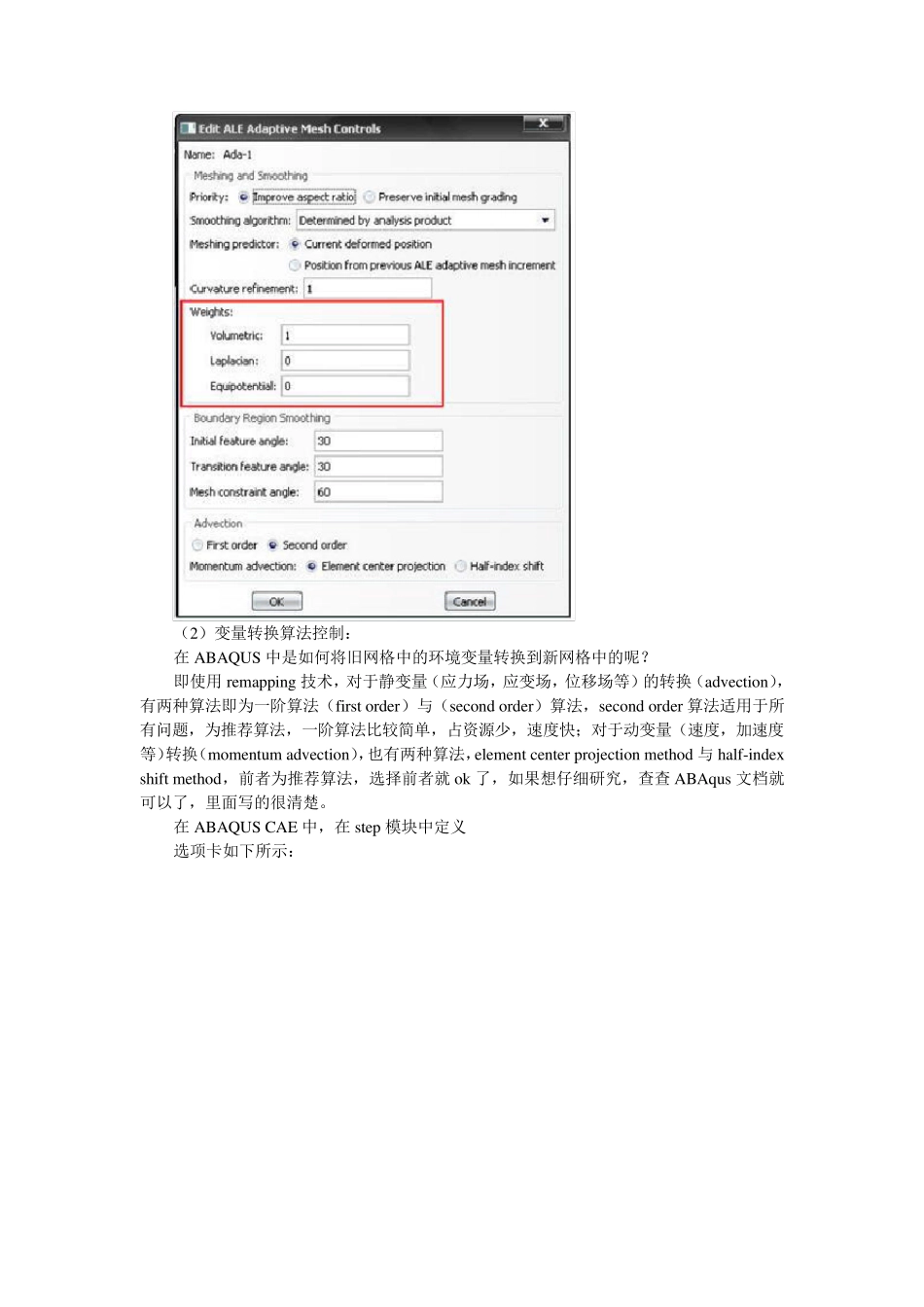
ALE 方法详解及各选项卡参数意义与设置 (ABAQUS/Explicit) 为了方便理解,先整体介绍一下ALE 网格自适应方法的基本过程 一个完整的ALE 过程可以分为若干个网格remesh 子过程,而每一次remesh 的过程可以分为一下两步: 1 生成一个新的网格(create a new mesh) 利用各种算法以及控制策略生成一个良好的网格 2 环境变量的转换(advection variales) 也就是将旧网格中的变量信息利用remapping 技术转换到新网格中,也有不同算法,其中包括静变量(应力场,应变场等)的转换与动变量(速度场,加速度场等)的转换 生成的新网格成功与否则在于对这两步的控制 首先来看第1 个大部分--对整个adaptive remesh 过程控制: 包括两个方面:一个是对adaptive remesh 过程的算法控制,另一个对adaptive mesh 过程强度的控制 1. 对adaptive remesh 的算法控制 算法控制包括两部分算法控制,其一为网格算法控制,其二为变量转换算法控制 (1)网格重画算法控制: 在ABAQUS 中是如何生成新网格的呢? 即使用网格扫掠技术(mesh sweep technique),每sweep 一次,生成一套新的网格。但是当你使用的算法不同时,sweep 出来的网格也是不同的,打个不是很恰当的比方:用不同的工具做同一件东西,做出来的质量与精度会不一样,同样,用不同的算法来sweep 网格,得到的网格质量也会不一样。 在ABAQUS 显示模块中,sweep 算法用英语来说就是mesh smoothing method,有三种算法来sweep 网格,如下所示: 1)体积算法(volume smoothing) 该算法十分健壮,为默认算法,再绝大多数情况下适用 2)拉普拉斯算法(laplacian smoothing) 耗费资源最少的算法,能力一般,作用与体积算法类似(一阶算法,类似于求平均值),对于曲率比较高的曲线曲面边界时,效果不是很理想 3).等位算法(equipotential smoothing) 比较复杂的算法,是基于拉普拉斯算法的解之上的算法,对曲率较大的曲线曲面边界效果较好,在节点被非结构化网格包围时,次算法为推荐算法,若节点被结构化网格包围,其效果与体积算法类似。 三种算法可以结合适用,利用权重值来定义,需要记住的是,三种算法各占的权值加起来必须等于1。 在ABAQUS CAE 中,在step 模块中定义 选项卡如下所示: (2)变量转换算法控制: 在ABAQUS 中是如何将旧网格中的环境变量转换到新网格中的呢? 即使用remapping 技术,对于静变量(应力场,应变场...