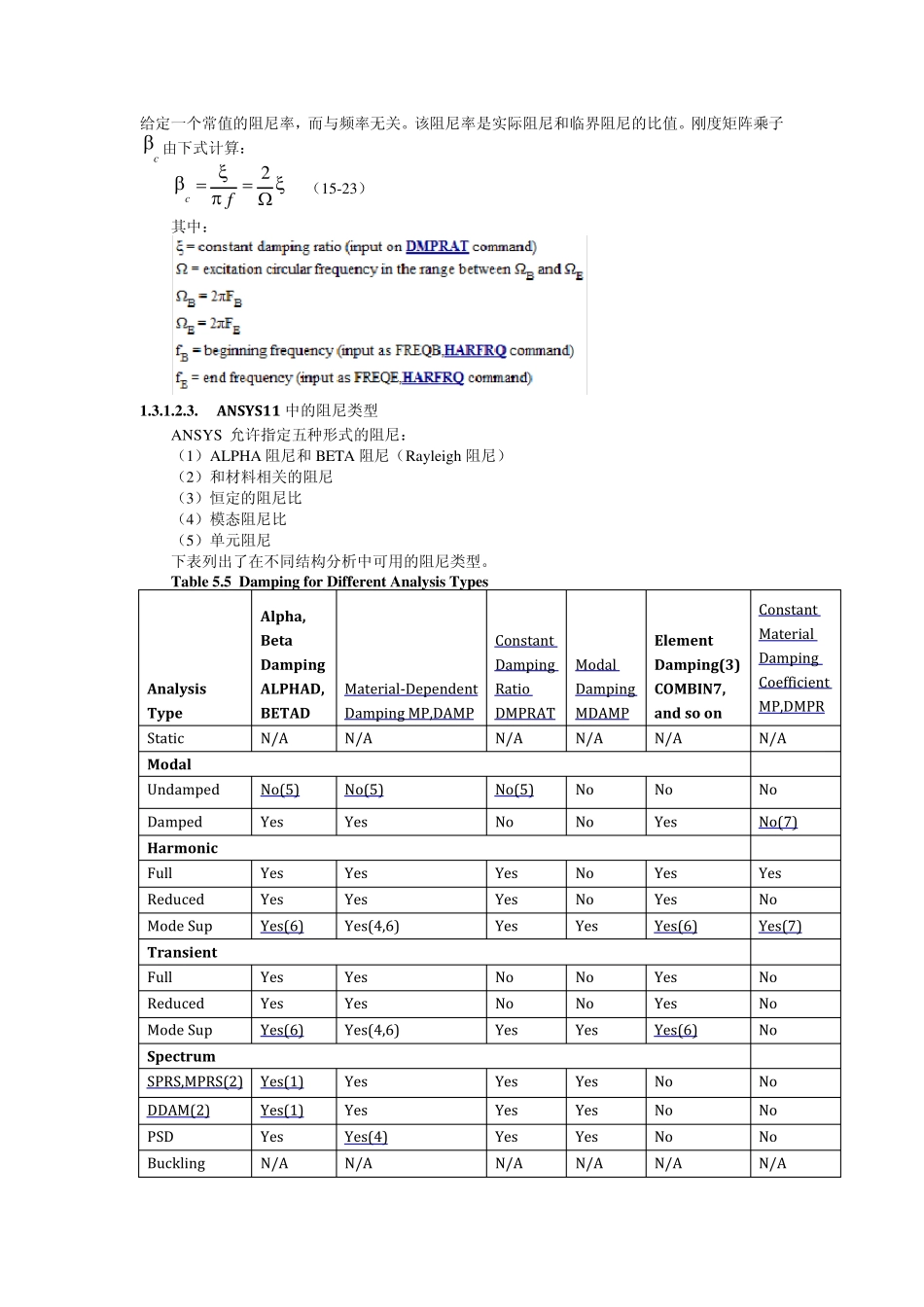
1.3.1. ANSYS 动力学分析中的矩阵 1.3.1.1. 质量矩阵[M] 动力学分析中需要质量矩阵[M]。ANSYS 有 2 种类型的质量矩阵:一致质量矩阵和集中质量矩阵。 一致(consistent)质量矩阵通过单元的形函数计算出来。矩阵的对角线和非对角线上一般均有元素值。一致质量矩阵是大多数单元的缺省选项。 集中(lumped )质量矩阵的质量被单元各节点平分,对角线上元素不为 0,非对角线上元素均为 0。通过分析选项来激活,命令 LUMPM,Key。默认 KEY=off,单元的一致质量矩阵,大多数单元的缺省选项。KEY=on,使用集中质量矩阵。其 GUI 为 Main Menu>Solution>Analysis Type>Analysis Options。 一致质量矩阵对大多数分析来说,精度比集中质量矩阵高,但其计算时间较长。 若结构在一个方向的尺寸与另两个方向相比很小时,可采用简化质量矩阵(如果可能得到的话)或集中质量矩阵例如细长的梁或很薄的壳。集中质量矩阵在大规模模型以及高速动力学如波传播问题上,具有较好的节省计算时间的优势。 1.3.1.2. 阻尼矩阵[C] 1.3.1.2.1. 阻尼的分类 阻尼的作用机制比较复杂。大多简化处理。阻尼的数值主要取决于材料、运动速度和振动频率。阻尼可分类如下:粘性阻尼,滞后或固体阻尼,库仑或干摩擦阻尼。 一、粘性阻尼 粘性阻尼一般物体在液体中运动时发生。由于阻尼力与速度成正比,比例常数 c 称作阻尼常数。通过规定阻尼比 ξ,Rayleigh 阻尼常数 α(后面将进行讨论),或定义带有阻尼矩阵的单元,可将粘性阻尼纳入考虑。 通常用 阻尼比 ξ(阻尼常数 c 对临界阻尼常数 cc*的比值)来量化表示粘性阻尼:ξ=c/cc。其中粘性阻尼 c,临界阻尼常数 cc。临界阻尼定义为出现振荡和非振荡行为之间的阻尼的极值, 此处阻尼比 = 1。对一个质量为 m ,频率为 w 的单自由度弹簧质量系统,cc = 2mw 。 注意: 阻尼比 ξ = 对于螺栓或铆钉链接结构常常为 2%到 15% 二、滞后和固体阻尼 滞后和固体阻尼是材料的固有特性,也称结构阻尼。在动力学分析中应该考虑,认识还不是很透彻,因此很难定量的确定。通过规定另一种 Rayleigh 阻尼常数 β(后面将进行讨论)可将滞后或固体阻尼纳入考虑 。 三、库仑或干摩擦阻尼 库仑或干摩擦阻尼是物体在干表面上滑动时产生的阻尼。阻尼力与垂直于表面的力成正比。比例常数 m 就是摩擦系数 。动力学分析中一般不予考虑 。通过规定带有摩擦性能的接触表面单元和间隙单元,可...