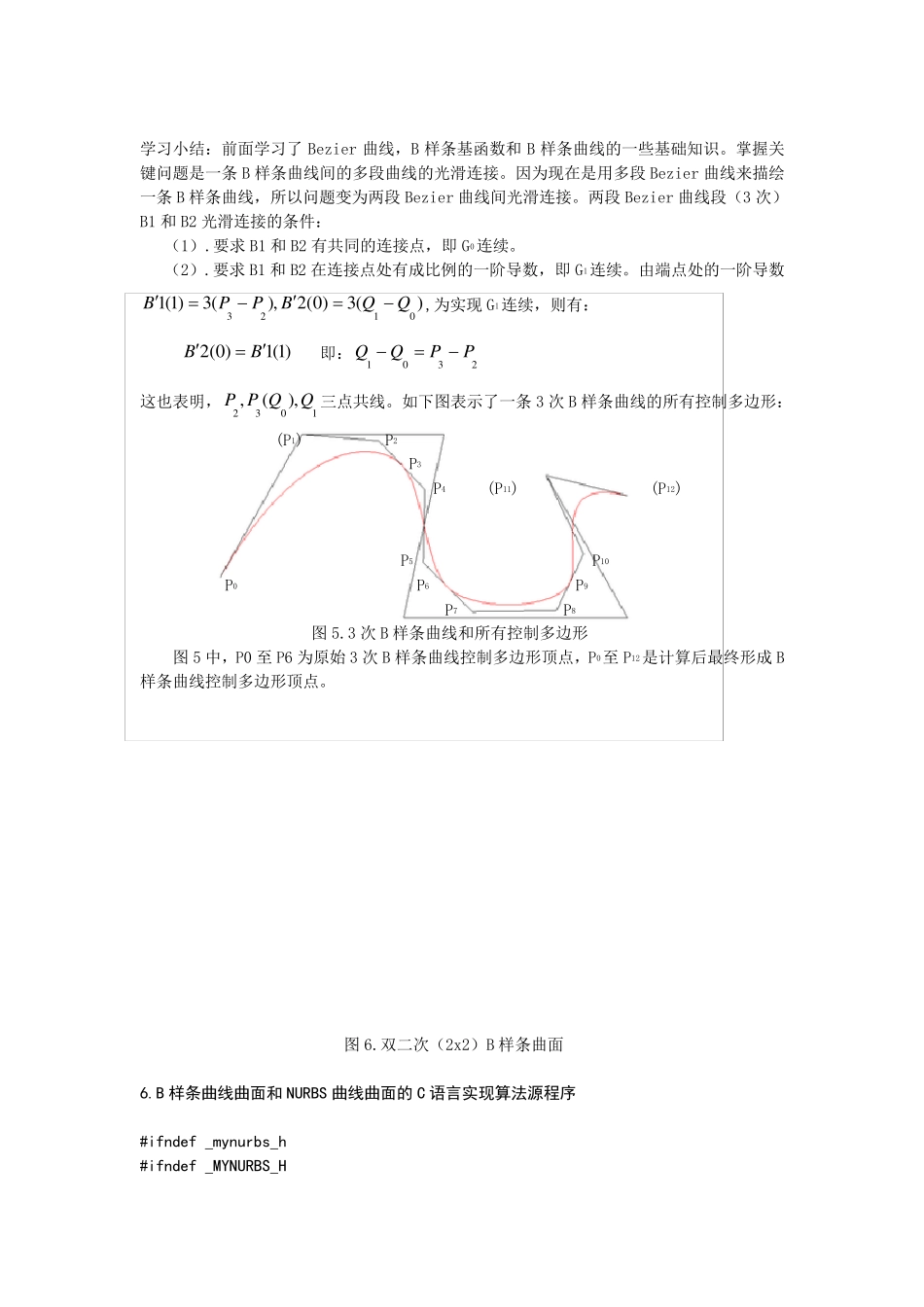
学习小结:前面学习了Bezier 曲线,B 样条基函数和B 样条曲线的一些基础知识。掌握关键问题是一条B 样条曲线间的多段曲线的光滑连接。因为现在是用多段 Bezier 曲线来描绘一条B 样条曲线,所以问题变为两段 Bezier 曲线间光滑连接。两段 Bezier 曲线段(3 次)B1 和B2 光滑连接的条件: (1).要求 B1 和B2 有共同的连接点,即 G0连续。 (2).要求 B1 和B2 在连接点处有成比例的一阶导数,即 G1连续。由端点处的一阶导数)(3)0(2),(3)1(10123QQBPPB,为实现 G1连续,则有: )1(1)0(2BB 即:2301PPQQ 这也表明,1032),(,QQPP三点共线。如下图表示了一条3 次 B 样条曲线的所有控制多边形: (P1) P2 P3 P4 (P11) (P12) P5 P10 P0 P6 P9 P7 P8 图 5.3 次 B 样条曲线和所有控制多边形 图 5 中,P0 至 P6 为原始 3 次 B 样条曲线控制多边形顶点,P0至 P12是计算后最终形成 B样条曲线控制多边形顶点。 图 6.双二次(2x2)B 样条曲面 6.B 样条曲线曲面和 NURBS 曲线曲面的 C 语言实现算法源程序 #ifndef _mynurbs_h #ifndef _MYNURBS_H #include "gl\gl.h" #include "math.h" //*-*-*-*-*-*-*-*-*-*-*-*-*-*-* B 样条基函数计算部分 *-*-*-*-*-*-*-*-*-*-*-*-*-* //确定参数u 所在的节点区间下标 //n=m-p-1 //m 为节点矢量 U[]的最大下标 //p 为 B 样条函数次数 int FindSource(int n,int p,float u,float U[]) { int low,high,mid; if(u==U[n+1])//特殊情况 return n; //进行二分搜索 low=p; high=n+1; mid=(int)(low+high)/2; while(uU[mid]) { if(u=U[mid]&&u=i-k;di--) { if(u>=U[di]&&u